It is often required to adjust the shape of a function by scaling to it or moving it so as to make it pass through certain points. For example, if we wanted to have a function $g$ with the same shape as the absolute value function $f(x)=|x|$, but for which $g(0)=3$, we would use the function $g(x)=|x|+3$.

In this section, we will discuss the four basic transformations you can do on any function $f$ to obtain a transformed function $g$:

• Vertical translation: $g(x) = f(x)+k$.
• Horizontal translation: $g(x) = f(x-h)$.
• Vertical scaling: $g(x) = Af(x)$.
• Horizontal scaling: $g(x) = f(ax)$.

By using these transformations we can move and stretch a generic function to give it any desired shape. 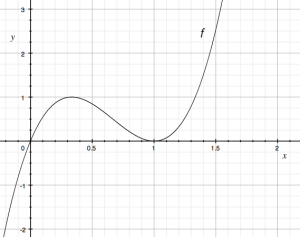We will illustrate all of the above transformations on the following function: \[ f(x) = 6.75(x^3 - 2x^2 +x). \] This function is chosen because it has distinctive features in both the horizontal and vertical directions. By observing the graph of this function, we see that its $x$-intercepts are at $x=0$ and $x=1$. The function $f$ also has a local maximum at $x=\frac{1}{3}$ and the height of the function there is $f(\frac{1}{3})=1$.

We can confirm the first observation mathematically by factoring the function as follows: \[ f(x) = 6.75x(x^2 - 2x +1) = 6.75x(x-1)^2, \] where we see clearly that $f(x)=0$ if $x=0$ (the $x$ factor kills it) or $x=1$ (the $(x-1)$ factor kills it).

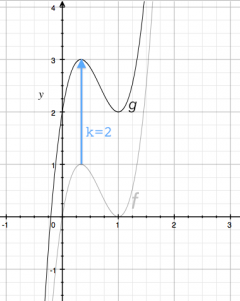
If we want to move a function $f$ up by $k$ units, we simply add $k$ to the function: \[ g(x) = f(x) + k. \] The function $g(x)$ will have exactly the same shape as $f(x)$ but it will be translated (the mathematical term for moved) upwards by $k$ units.

Recall the function $f(x) = 6.75(x^3 - 2x^2 +x)$. If we wanted to move the function up by $k=2$ units, we would obtain: \[ g(x) = f(x)+2 = 6.75(x^3 - 2x^2 +x) + 2, \] and the graph of $g(x)$ will be as shown on the right. The original function $f(x)$ crossed the $x$-axis at $x=0$, so we had $f(0)=0$. The transformed function must therefore obey $g(0)=2$. The maximum at $x=\frac{1}{3}$ has similarly shifted in value from $f(\frac{1}{3})=1$ to $g(\frac{1}{3})=3$.

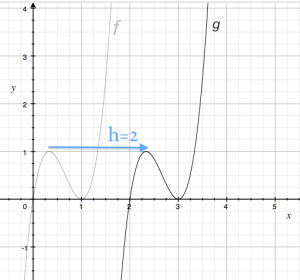
We can move a function $f$ to the right by $h$ units by subtracting $h$ from $x$ and using that as the input argument: \[ g(x) = f(x-h). \] The point $(0,f(0))$ on $f(x)$ will now correspond to the point $(h,g(h))$ on $g(x)$.

Consider the graph on the right which shows the function $f(x)= 6.75(x^3 - 2x^2 +x)$ as well as the function $g(x)$ which is shifted to the right by $h=2$ units: \[ g(x) = f(x-2) = 6.75\left[ (x-2)^3 - 2(x-2)^2 +(x-2) \right]. \]

The original function $f$ had $f(0)=0$ and $f(1)=0$ so the new function $g(x)$ must have $g(2)=0$ and $g(3)=0$. The maximum at $x=\frac{1}{3}$ has similarly shifted by two units to the right $g(2+\frac{1}{3})=1$.

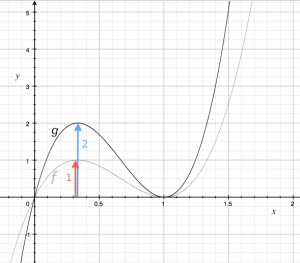
To stretch or compress the shape of a function vertically, we can multiply it by some constant $A$ and obtain: \[ g(x) = Af(x). \] If $|A|>1$, the function will be stretched, and if $|A|<1$ the function will be compressed. If $A$ is negative, the function will also be flipped upside down (reflection through the $x$-axis).

There is an important difference between vertical translation and vertical scaling. Translation moves all the points of the function the same amount, whereas scaling moves each point proportionally to how far it is from the $x$ axis.

On the right, we see the graph on the function $f(x)= 6.75(x^3 - 2x^2 +x)$ and the function $g(x)$ which is equal to $f(x)$ stretched vertically by a factor of $A=2$: \[ g(x) = 2f(x) = 13.5(x^3 - 2x^2 +x). \]

The $x$-intercepts $f(0)=0$ and $f(1)=0$ didn't move: $g(0)=0$ and $g(1)=0$. The maximum at $x=\frac{1}{3}$ has now doubled in value $g(\frac{1}{3})=2$. Indeed, all values of $f(x)$ have been stretched upwards by a factor of 2, as can be verified with the point $f(1.5)=2.5$ which has become $g(1.5)=5$.

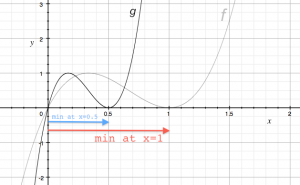
To stretch or compress a function horizontally we can multiply the input value by some constant $a$ to obtain: \[ g(x) = f(ax). \] If $|a|>1$, the function will be compressed, and if $|a|<1$ the function will be stretched. Note that the behaviour here is the opposite of the vertical case. If $a$ is a negative number, the function will also be flipped horizontally (reflection through the $y$-axis).

The graph on the right shows the function $f(x)= 6.75(x^3 - 2x^2 +x)$ and the function $g(x)$ which is $f(x)$ compressed horizontally by a factor of $a=2$: \[ g(x) = f(2x) =6.75\left[ (2x)^3 - 2(2x)^2 +(2x)\right]. \]

The $x$-intercept $f(0)=0$ didn't move since it is on the $y$-axis. The $x$-intercept $f(1)=0$ did move however and we now have $g(0.5)=0$. The maximum at $x=\frac{1}{3}$ has now moved to $g(\frac{1}{6})=1$. All values of $f(x)$ have been compressed towards the $y$-axis by a factor of 2.