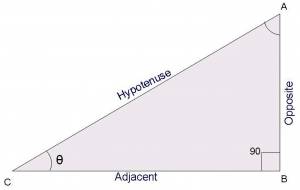
Put together any three lines and you get a triangle. In particular, if the triangle has one of its angles equal to $90^\circ$, we call this a right angle triangle.

In this section we are going to discuss right angle triangles in great detail and get used to their properties. You will learn how to use fancy Greek words like sinus, cosinus and tangent in order to refer to the various ratios of lengths in the triangle.

Understanding triangles and the trigonometric functions associated with them will be of fundamental importance for your later understanding of mathematics subjects like vectors and complex numbers and physics subjects like oscillations and waves.

• $A,B,C$: the three vertices of the triangle
• $\theta$: the angle at the vertex $C$. Angles can be measured in degrees or radians.
• $\text{opp} \equiv \overline{AB}$: the length of the opposite side to $\theta$
• $\text{adj} \equiv \overline{BC}$: the length of side adjacent to $\theta$
• $\text{hyp} \equiv \overline{AC}$: the hypotenuse is longest side in the triangle
• $h$: the “height” of the triangle (in this case $h = \text{opp} = \overline{AB}$)
• $\sin\theta \equiv \frac{\text{opp}}{\text{hyp}}$: the sinus of theta, is the ratio of the lengths of the opposite side and the hypotenuse
• $\cos\theta \equiv \frac{\text{adj}}{\text{hyp}}$: the cosinus of theta, is the ratio of the adjacent and the hypotenuse lengths
• $\tan\theta \equiv \frac{\sin\theta}{\cos\theta} \equiv \frac{\text{opp}}{\text{adj}}$: the tangent is the ratio of the opposite divided by the adjacent

In a right angle triangle, the length of the hypotenuse squared is equal to the sum of the squares of the lengths of the other sides: \[ |\text{adj}|^2 + |\text{opp}|^2 = |\text{hyp}|^2. \]

If we divide both sides of the above equation by $|\text{hyp}|^2$ we obtain \[ \frac{|\text{adj}|^2}{ |\text{hyp}|^2 } + \frac{|\text{opp}|^2}{ |\text{hyp}|^2 } = 1, \] which can be rewritten as: \[ \cos^2\theta \ + \sin^2\theta = 1. \] This is a powerful trigonometric identity: a relationship between $\sin$ and $\cos$.

Meet the trigonometric functions, or trigs for short. These are your new friends. Don't be shy now, say hello to them.

“Hello.”
“Hi.”
“Soooooo, you are like functions right?”
“Yep,” sin and cos reply in chorus.
“Okkkkkk, so what do you do?”
“Who me?”, asks cos, “well I tell the ratio.. Hmm.. wait, were you asking what I do as a function or specifically what I do?”
“Both I guess?”
“Ok so as a function, I take angles as inputs and I give ratios as answers. More specifically, I tell you how wide a triangle with that angle will be,” says cos all in one breath.
“What do you mean wide?”, you ask.
“Oh yeah, I forgot to say, the triangle has to have hypotenuse of length 1. So you see what happens is that, there is like a point $P$ that moves around on a circle of radius 1, and we imagine a triangle that has corners the origin, the point $P$ and the point on the $x$ axis that is right below the point $P$.”
“I am not sure I get it,” you confess.
“Let me try to explain then”, says sin, “cos is always the one to start off big and confuse people. I will start from zero.”
“OK. Sure. I mean I just don't see what circle cos is talking about.”
“Look on the next page, you will see a circle. The unit circle because it has radius one. You see it yes?”
“Yes.”
“The circle thing really cool. Imagine a point $P$ which stators from the point $P(0)=(1,0)$ and moves in a circle of radius one. The $x$ and $y$ coordinates of the point $P(\theta)=(P_x(\theta),\ P_y(\theta))$ as a function of $\theta$ are given by: \[ P(\theta)=(P_x(\theta),\ P_y(\theta)) = (\cos\theta, \ \sin\theta ). \] So, either you think of us in the context of triangles or you think of us in the context of the unit circle.”
“OK. Cool. I kind of get it,” you say it to keep conversation, but in reality you are all weirded out. Talking functions? “Well, thank you guys. It was nice to meet you, but you know I have to get going now, so see you later,” you say to get out the situation.
“OK. Peace out,” says sin, “anyways we are done here, since I told you the most important things.”
“See you later,” says cos.

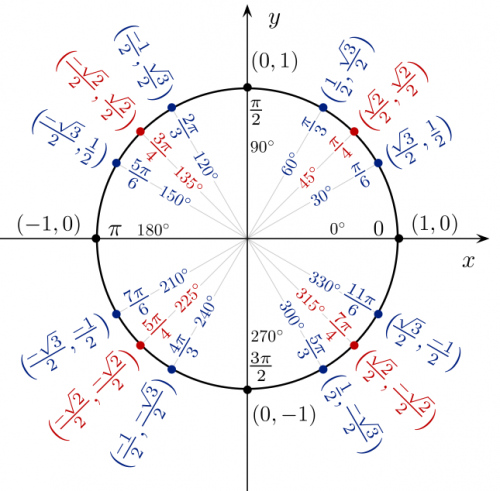
You should be familiar with the values of $\sin$ and $\cos$ for all the angles that are multiples of $\frac{\pi}{6}$ ($30^\circ$) or $\frac{\pi}{4}$ ($45^\circ$). All of them are shown in the diagram below. For each angle, the $x$ coordinate (the first number in the brackets below) is $\cos$ and the $y$ coordinate is $\sin$.

You might think that there is too much to remember. “Dude”, you say, “I was listening to your advice until now and learning, but now you are telling me to remember all those values with so many square roots in them. How am I to remember all of that?”

Actually, you just have to memorize one fact: \[ \sin(30^\circ) = \sin\!\!\left( \frac{\pi}{6} \right) = \frac{1}{2}. \]

My dad was like “You have to put this in the book”, and he is right. You can figure out all the other angles from this one. Let's start with $\cos(30^\circ)$. We know that the point $P$ on the unit circle at $30^\circ$ has vertical coordinate $\frac{1}{2}=\sin(30^\circ)$, and that by definition the horizontal component is the $\cos$ quantity we are looking for: \[ P = (\cos(30^\circ), \sin(30^\circ) ). \]

The key fact about the unit circle, is that all the points or it are at distance one from the centre. So knowing that $P$ is on the unit circle, and the value of $\sin(30^\circ)$, we can solve for $\cos(30^\circ)$. Indeed we start from the identity: \[ \cos^2\theta \ + \sin^2\theta = 1, \] which is true for all angles $\theta$. Moving things around, we obtain: \[ \cos(30^\circ) = \sqrt{ 1 - \sin^2(30^\circ) } = \sqrt{ 1 - \frac{1}{4} } = \sqrt{ \frac{3}{4} } = \frac{\sqrt{3}}{2}. \]

To get the values of $\cos(60^\circ)$ and $\sin(60^\circ)$, observe the symmetry of the circle. Sixty degrees measured from the $x$ axis, is the same as thirty degrees measured from the $y$ axis. So immediately you know that $\cos(60^\circ)=\sin(30^\circ)=\frac{1}{2}$. Therefore, it must be that $\sin(60^\circ) = \frac{\sqrt{3}}{2}$.

To get the values of sin and cos for angles that are multiples of $45^\circ$, we need to find the value $a$ such that \[ a^2 + a^2 = 1, \] since at $45^\circ$ both the horizontal part and the vertical part will be of the same length. The answer is obviously $a=\frac{1}{\sqrt{2}}$, but because people don't like to see square roots in the denominator we have to write: \[ \frac{\sqrt{2}}{2} = \cos(45^\circ) = \sin(45^\circ). \]

All of the other angles in the circle are just like the above three, but they have a negative sign in one or more of the components. Don't memorize them, but if you ever need one of their values draw a little circle and use the symmetry of the circle to find them. For example, $150^\circ$ is just like $30^\circ$, except the $x$ component is negative.

Consider now a point $Q(\theta)$ at an angle of $\theta$ on a circle of radius $R\neq1$. How can we find the $x$ and $y$ coordinates of the point $Q(\theta)$?

We saw that the coefficients $\cos\theta$ and $\sin\theta$ correspond the $x$ and $y$ coordinates of a point on the unit circle ($R=1)$. To obtain the coordinates for a point on a circle of radius $R$ we must scale the coordinates by a factor of $R$: \[ Q(\theta) = (Q_x(\theta), Q_y(\theta) ) = ( R\cos\theta, R\sin\theta ). \]

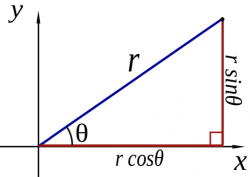The take home message is that the functions $\cos\theta$ and $\sin\theta$ are generally useful for finding the “horizontal” and “vertical” components of any length $r$.

From this point on in the book, we will always talk about the length of the adjacent side as $r_x=r\cos\theta$ and the opposite side as $r_y = r\sin\theta$. It is extremely important that you get comfortable with this notation.

The reasoning behind the above calculations is as follows: \[ \begin{align*} \cos\theta \equiv \frac{\text{adj}}{\text{hyp}} = \frac{r_x}{r} & \quad \Rightarrow \quad r_x = r \cos\theta, \nl \sin\theta \equiv \frac{\text{opp}}{\text{hyp}}=\frac{r_y}{r} & \quad \Rightarrow \quad r_y = r\sin\theta. \end{align*} \]

Make sure your calculator is set to the right units for angles. If you wanted to compute the sinus of 30 degrees what should you type into your calculator?

If you calculator is set to degrees then simply type sin + 30 + =.

But what if your calculator is set to radians? You have two options:

1. Change the mode of the calculator so it works in degrees.
2. Convert $30^\circ$ to radians

\[ 30 \ [^\circ] \times \frac{ 2\pi \ [\text{rad}] }{ 360 \ [^\circ] } = \frac{\pi}{6} \ \text{[rad]}, \]

  so you should type ''sin'' + $\pi$ + ''/'' + ''6'' + ''='' on your calculator.