The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Geometry
Triangles
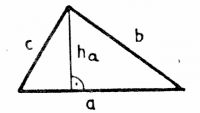 The area of a triangle is equal to $\frac{1}{2}$
times the length of the base times the height:
\[
A = \frac{1}{2} a h_a.
\]
Note that $h_a$ is the height of the triangle relative to the side $a$.
The area of a triangle is equal to $\frac{1}{2}$
times the length of the base times the height:
\[
A = \frac{1}{2} a h_a.
\]
Note that $h_a$ is the height of the triangle relative to the side $a$.
The perimeter of the triangle is: \[ P = a + b + c. \]
Consider now a triangle with internal angles $\alpha$, $\beta$ and $\gamma$. The sum of the inner angles in any triangle is equal to two right angles: $\alpha+\beta+\gamma=180^\circ$.
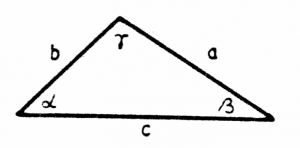 The sine law is:
\[
\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)},
\]
where $\alpha$ is the angle opposite to $a$, $\beta$ is the angle opposite to $b$ and $\gamma$ is the angle opposite to $c$.
The sine law is:
\[
\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)},
\]
where $\alpha$ is the angle opposite to $a$, $\beta$ is the angle opposite to $b$ and $\gamma$ is the angle opposite to $c$.
The cosine rules are: \[ \begin{align} a^2 & =b^2+c^2-2bc\cos(\alpha), \nl b^2 & =a^2+c^2-2ac\cos(\beta), \nl c^2 & =a^2+b^2-2ab\cos(\gamma). \end{align} \]
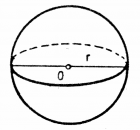
Sphere
A sphere is described by the equation \[ x^2 + y^2 + z^2 = r^2. \]
Surface area: \[ A = 4\pi r^2. \]
Volume: \[ V = \frac{4}{3}\pi r^3. \]
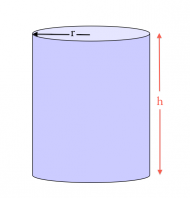
Cylinder
The surface area of a cylinder consists of the top and bottom circular surfaces plus the area of the side of the cylinder: \[ A = 2 \left( \pi r^2 \right) + (2\pi r) h. \]
The volume is given by product of the area of the base times the height of the cylinder: \[ V = \left(\pi r^2 \right)h. \]
Example
You open the hood of your car and see 2.0L written on top of the engine. The 2[L] refers to the total volume of the four pistons, which are cylindrical in shape. You look in the owner's manual and find out that the diameter of each piston (bore) is 87.5[mm] and the height of each piston (stroke) is 83.1[mm]. Verify that the total volume of the cylinder displacement of your engine is indeed 1998789[mm$^3$] $\approx 2$[L].
Links
[ A formula for calculating the distance between two points on a sphere ]
http://www.movable-type.co.uk/scripts/latlong.html