The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Exponential
Definition
\[ f(x)=Ae^{\gamma x}. \]
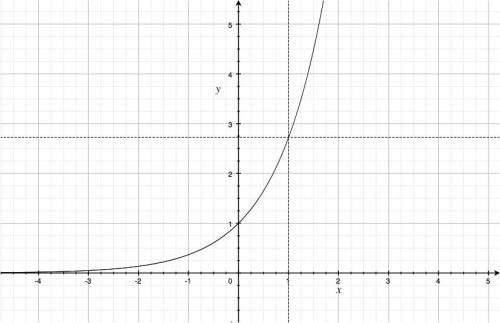
Graph
The exponential function graph:
Parameters
- $A$: the initial value, $A=f(0)$. The graph shows the case $A=1$.
- $\gamma$: the rate of the exponential.
For $\gamma > 0$ the function is increasing.
for $\gamma < 0$ the function is decreasing
and tends to zero for large values of $x$.
The case $\gamma=0$ is special since $e^{0}=1$,
and so the exponential becomes the constant function $f(x)=A$.
The graph shows the case $\gamma=1$.
Properties
- The number $e$ is related to the following limit argument
\[ e = \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n, \]
which can be interpreted as a formula for compounding interest.
The limit as $n$ goes to infinity refers to a scenario when
the compounding is performed infinitely often.
* The derivative (slope) of the exponential function is
equal to the exponential function:
\[
f(x) = e^x \ \ \Rightarrow \ \ f'(x)=e^x.
\]
In function $e^x$ is equal to its derivative: $f(x)=f'(x)$.
Links
[ the exponential function $2^x$ for the naturals $x \in \mathbb{N}$ can easily be evaluated by drawing ]
http://www.youtube.com/watch?v=e4MSN6IImpI