The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
General quadratic function
Definition
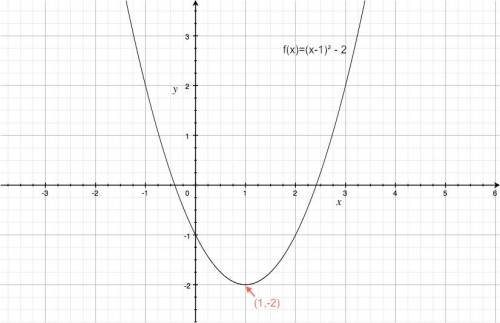
The general quadratic function has the following form: \[ f(x) = A(x-h)^2 + k, \] where $x$ is the input and $A,h$ and $k$ are the parameters.
Parameters
- $A$: slope multiplier.
- The larger the value of $A$ the steeper the slope.
- If $A<0$ (negative), then the function opens downwards.
- $h$: horizontal displacement of the function centre. Notice that subtracting a
number inside the bracket $(\ )^2$ (i.e. positive $h$) makes the function go to the right.
- $k$: vertical displacement of the function.
If a quadratic crosses the $x$-axis, then it can be written in factored form \[ f(x) = (x-a)(x-b), \] where $a$ and $b$ are the two roots.
Another very common way of writing a quadratic function is \[ f(x) = Ax^2 + Bx + C. \]
Properties
- There is a unique parabola that passes through any three points $(x_1,y_1),$ $(x_2,y_2)$ and $(x_3,y_3)$ if
the points have different $x$ coordinates $x_1 \neq x_2$, $x_2 \neq x_3$ and $x_1 \neq x_3$.
- The derivative of $f(x)=Ax^2 + Bx + C$ is $f'(x)=2Ax + B$.
Graph
When $h=1$ (one unit shifted to the right) and $k=-2$ (two units shifted downwards), we get the following graph:
