Using version control is very useful for storing text documents like papers and books. It’s amazing how easy it is to track changes to documents, and communicate these changes with other authors. In my career as a researcher, I’ve had the chance to initiate many colleagues to the use of mercurial and git for storing paper manuscripts. Also, when working on my math books, I’ve had the fortune to work with an editor who understands version control and performed her edits directly to the books’ source repo. This blog post is a brainstorming session on the what a git user interface specific to author’s needs could look like.
Git for authors
Linear algebra book alpha release
The No bullshit guide to linear algebra is almost finished. I know I have been saying something along these lines for almost two years now, but it’s for real this time. Read below for a general preview of the new chapters, and the story about why it took so long to write them.
Progress on linear algebra
It has been almost a year now since the linear algebra book is “almost finished.” I don’t have any real, legitimate excuse for this delay. The first seven chapters are now done, and have been thoroughly edited and finalized. What is taking forever is finishing the applications chapters, which I’m being super slow at. The only thing I can say in my defense is that there are A LOT of applications of linear algebra, and writing about even a small part of them takes a lot of time.
Okay, so what’s coming?
- The applications chapter covers topics in cryptography, error correcting codes, network coding, Fourier analysis, as well as the standard topics of least-squares fitting and solving equations.
- I’ve decided to cut the section on linear programming (the simplex method). Despite trying very hard to make the material interesting and concise, I wasn’t able to. It’s just a boring-as-hell topic, so I don’t see the point of including it in the book. The text is almost done though, so I’ll probably release it as a free PDF for students who have to do this in their class.
- I added a new chapter on probability theory, Markov chains, and quantum mechanics. This will be optional reading, but I think I managed to fit all the important things (Dirac notation, postulates of QM, quantum gates, examples, etc.) to make a decent introduction to the subject.
The final version of the book will be around 450 pages, which is kind of chunky. Not cool, but I think it’s good to include the chapter on probability theory and QM, even though they are not “core” for a linear algebra class. What do y’all think? Should I include prob. theory and QM or cut it to make the book shorter by 60 pages (reply in the comments or by email)?
The other good news™ is my friend agreed to prepare exercises and problems for the book, which means the first edition (v1.0) will be very solid and complete. Estimated time of release is circa February 1st. Dear readers, I apologize for the massive delays. Hang in there, LA is coming!
Binary search in three languages
Hola! Regardons ensemble un peu de code. The binary_search algorithm. It will get a little technical, pero no es mucho complicado. A ver. En ingles. En anglais, parce que le code—ça va foule mieux en anglais.
Assume you’re given a array of integers sorted in increasing order [3,6,19,21,87]. You job is to write a “search” function that returns the 0-based index of query value, or -1 if val is not in array.
Binary search algorithm
The “usual” algorithm use the start and finish pointers in a weird way, which I found difficult to understand, so I wrote another one. The invariant “we’ve already checked the limits” feels more logical to me.
In JavaScript
In JavaScript the code for the binary search strategy is as follows:
SearchableArray.prototype.binary_search = function (val) {
var data = this.data;
if (data.length === 0) return -1;
if (data[0] === val) return 0;
if (data[data.length-1] === val) return data.length -1 ;
var bin_search_limits = function(start,finish) {
// invariant: data[start] and data[finish] have been checked already
var mid;
//console.log(start, finish);
if (start === finish || start+1 === finish)
return -1;
mid = start + Math.floor((finish-start)/2);
if (data[mid]===val) {
return mid;
} else if (data[mid] < val) {
return bin_search_limits(mid,finish);
} else if (data[mid] > val) {
return bin_search_limits(start,mid);
}
};
return bin_search_limits(0, data.length-1);
};
The full javascript code (with tests;) is here.
In C
It was surprisingly easy to transform the JavaScript code into C. See the code and some basic tests here. The main functions essentially the same:
int bin_search_limits(int *data, int start, int finish, int val) {
// invariant: data[start] and data[finish] have been checked already
int mid;
if (start == finish || start+1 == finish)
return -1;
mid = start + (finish-start)/2;
if (data[mid]==val) {
return mid;
} else if (data[mid] < val) {
return bin_search_limits(data,mid,finish, val);
} else if (data[mid] > val) {
return bin_search_limits(data,start,mid, val);
}
};
int binary_search(int *data, int length, int val) {
if (length == 0) return -1;
if (data[0] == val) return 0;
if (data[length-1] == val) return length-1;
return bin_search_limits(data,0,length-1, val);
};
In python
The pleasure of implementing binary search in python is left to the reader.
I’ve got to go code learn how to make a hash function to make the C test suite go faster 😉
Linear algebra applications
I spent the last month at the chalet in Petkovo, the village where my grandfather is from. Check out the view from my office:
I have good progress to report on the linear algebra book. Sandy (my editor) has gone through the first few chapters and looks on track to finish editing the book by the end of October, which means the NO BS guide to LA will be available in print soon.
On my side, I’ve been working on the applications chapter. In this chapter I discuss all the cool things you can do using linear algebra. The topics covered include linear programming, error correcting codes, solving for the voltages in electric circuits, and other applications to economics and science. It really feels good to be able to discuss all these applications, and substantiate the claim I make in the book’s introduction, namely, that learning linear algebra will open many doors for the reader.
In other news, I think I’ve finally found a civilized way to generate html and .epub versions of the book: polytexnic, which is part of the softcover platform for self-publishers. Here’s a quote from the documentation:
The real challenge is producing EPUB and MOBI output. The trick is to (1) create a self-contained HTML page with embedded math, (2) include the amazing MathJax JavaScript library, configured to render math as SVG images, (3) hit the page with the headless PhantomJS browser to force MathJax to render the math (including any equation numbers) as SVGs, (4) extract self-contained SVGs from the rendered pages, and (5) use Inkscape to convert the SVGs to PNGs for inclusion in EPUB and MOBI books. Easy, right? In fact, no—it was excruciating and required excessive amounts of profanity to achieve. But it’s done, so ha.
Stay tuned for .epub version of the books in the No BS guide series.
Math makes you cry? Try SymPy!
This summer I wrote a short SymPy tutorial that illustrates how a computer
algebra system can help you understand math and physics. Using SymPy you can solve all kinds of math problems, painlessly.
Check it:
Sympy tutorial (PDF, 12 pages)
Print this out, and try the examples using live.sympy.org. The topics covered are: high school math, calculus, mechanics, and linear algebra.
SymPy makes all math and physics calculation easy to handle, it can even make them fun! Learn the commands and you’ll do well on all your homework problems. Best of all, sympy is free and open source software so your learning and your calculations won’t cost you a dime!
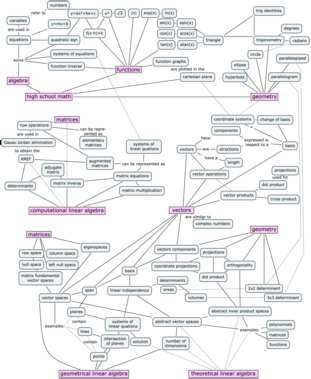
Linear algebra concept maps
I spent the last week drawing. More specifically, drawing in concept space. Drawing concept maps for the linear algebra book.
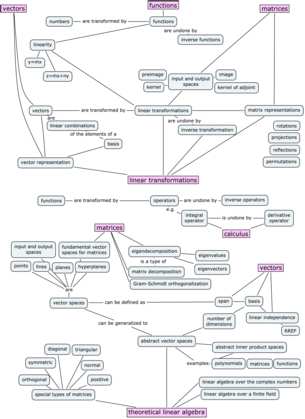
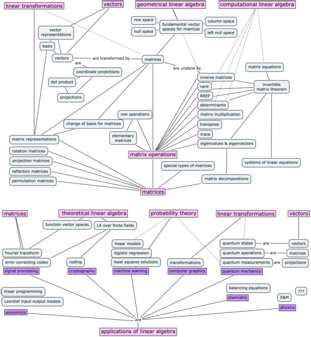
Without going into too much details, the context is that the old concept map was too overloaded with information, so I decided to redo it. I had to split the concept map on three pages, because there’s a lot of stuff to cover. Check it out.
Math basics and how they relate to geometric and computational aspects of linear algebra
The skills from high school math you need to “import” to your study of linear algebra are geometry, functions, and the tricks for solving systems of equations (e.g. the values $x$ and $y$ that simultaneously satisfy the equations $x+y=3$ and $3x+y=5$ are $x=1$ and $y=2$.)
The first thing you’ll learn in linear algebra is the Gauss–Jordan elimination procedure, which is a systematic approach for solving systems of $n$ equations with $n$ unknowns. You’ll also learn how to compute matrix products, matrix determinants, and matrix inverses. This is all part of Chapter 3 in the book.
In Chapter 4, we’ll learn about vector spaces and subspaces. Specifically, we’ll discuss points in $\mathbb{R}^3$, lines in $\mathbb{R}^3$, planes in $\mathbb{R}^3$, and $\mathbb{R}^3$ itself. The basic computational skills you picked up in Chapter 3 can be used to solve interesting geometric problems in vectors spaces with any number of dimensions $\mathbb{R}^n$.
Linear transformations and theoretical topics
The concept of a linear transformation $T:\mathbb{R}^n \to \mathbb{R}^m$ is the extension of the idea of a function of a real variable $f:\mathbb{R} \to \mathbb{R}$. Linear transformations are linear functions that take $n$-vectors as inputs and produce $m$-vectors as outputs.
Understanding linear transformations is synonymous with understanding linear algebra. There are many properties of a linear transformation that we might want to study. The practical side of linear transformations is their nature as a vector-upgrade to your existing skill set of modelling the world with functions. You’ll also learn how to study, categorize, and understand linear transformations using new theoretical tools like eigenvalues and eigenvectors.
Matrices and applications
Another fundamental idea in linear algebra is the equivalence between linear transformations $T:\mathbb{R}^n \to \mathbb{R}^m$ and matrices $M \in \mathbb{R}^{m\times n}$. Specifically, the abstract idea of a linear transformation $T:\mathbb{R}^n \to \mathbb{R}^m$, when we fix a particular choice of basis $B_i$ for the input space and $B_o$ for the output space of $T$, can be represented as a matrix of coefficients $_{B_o}[M_T]_{B_i} \in \mathbb{R}^{m\times n}$. The precise mathematical term for this equivalence is isomorphism. The isomorphism between linear transformations and their matrix representations means we can characterize the properties of a linear transformation by analyzing its matrix representation.
Chapter 7 in the book contains a collection of short “applications essays” that describe how linear algebra is applied to various domains of science and business. Chapter 8 is a mini-intro to probability theory and Chapter 9 is an intro course on quantum mechanics. All the applications are completely optional, but I guarantee you’ll enjoy reading them. The power of linear algebra made manifest.
If you’re a seasoned blog reader, and you just finished reading this post, I know what you’re feeling… a moment of anxiety goes over you—is a popup asking you to sign up going to show up from somewhere, is there going to be a call to action of some sort?
Nope.
Problem sets ready
Sometime in mid-December I set out to create problem sets for the book. My friend Nizar Kezzo offered to help me write the exercises for Chapter 2 and Chapter 4 and I made a plan to modernize the calculus questions a bit and quickly write a few more questions and be done in a couple of weeks.
That was four months ago! Clearly, I was optimistic (read unrealistic) about my productivity. Nizar did his part right on schedule, but it took me forever to write nice questions for the other chapters and to proofread everything. After all, if the book is no bullshit, the problem sets must also be no bullshit. I’m quite happy with the results!
noBS problem sets: letter format or 2up format.
Please, if you find any typos or mistakes in the problem sets, drop me a line so I can fix them before v4.1 goes to print.
Tools
In addition to work on the problem sets, I also made some updates to the main text. I also developed some scripts to use in combination with latexdiff to filter only pages with changes. This automation saved me a lot of time as I didn’t have to page through 400pp of text, but only see the subset of the pages that had changes in them.
If you would like to see the changes made to the book from v4.0 to v4.1 beta, check out noBSdiff_v4.0_v4.1beta.pdf.
Future
Today I handed over the problems to my editor and once she has taken a look at them, I’ll merge the problems into the book and release v4.1. The coming months will be focussed on the business side. I know I keep saying that, but now I think the book is solid and complete so I will be much more confident when dealing with distributors and bookstores. Let’s scale this!
Linear algebra tutorial in four pages
I just pushed an update to the Linear algebra explained in four pages tutorial.
Anyone who has an exam with lots of $A\vec{x}=\vec{b}$ stuff on it coming up should check it out because it covers: vector operations, matrix operations, linear transformations(matrix-vector product, fundamental vector spaces, matrix representation), solving systems of linear equations (the RREF stuff), matrix inverse, eigenvalues.
UPDATE: I found another excellent tutorial which I think you should also read, especially if you are a visual person. A Geometric Review of Linear Algebra by Prof. Eero P. Simoncelli (discuss on HN if you are a procrastinating person). If you’re a studious person, you’ll also go to en.wikibooks.org/wiki/Linear_Algebra and practice solving problems. To become a powerful person, don’t look at the solution until you’ve attempted the problem (with pen and paper) for at least five minutes.
UPDATE: I found some other useful short tutorials, like this short review of linear algebra from Stanford and another one from Boulder which both cover interesting details and bring a new perspective.
Network protocols discussion
There is an interesting discussion about network protocols going on at hacker news. In just a few posts some very knowledgeable people stepped in to explain what is going on. I saved the URL in the Links section of /miniref/comp/network_programming but it made me think about how much better informal explanation is to formal explanations.
Here you have hackers talking to other hackers. Whether it is a javascript-wielding young blood or an old dude who writes server-side stuff in C, all these people need to send data on the network and know of some some protocols for doing that: TCP:HTTP for web dev mostly while systems people probably think more in terms of (TCP:*).
Everyone jumps in to check what is going on on the HN discussion. And then suddenly learning happens. The discussion is a bit disorganized (shown as discussion tree) but let me give you the walk through.
First chetanahuja tells it like it is:
IP layer is for addressing nodes on the internet and routing packets to them in a stateless manner (more or less… I’m not counting routing table caches and such as “state”). TCP […] are built on top of the IP layer to provide reliable end-to-end data transfers in some sort of session based mechanism.
The key thing to know is that IP is a best-effort protocol. If you send an IP packet from computer A to computer B, the network will try to deliver it but there are not guarantees that it will succeed. No problem though, we can build a reliable protocol (the Transmission Control Protocol) on top of the unreliable one. This is why the Internet is usually referred to as TCP/IP, not just IP even thought IP stands for Internet Protocol. TCP/IP is the internet made reliable.
TCP is important because it allows for reliable communication: When A sends some data to B, B will reply with an ACKnowledge packet to tell A when he received the data. Reliability comes from the fact that A will retransmit all the packets for which no ACKs are received (the sender assumes these packets got lost). The other thing the TCP protocol gives you is the notion of a port — a multiplexing mechanism for running multiple networks services on the same machine. Port 80 is the HTTP port (web browsing). When you type in 11.22.33.44 into the browser, your browser will send a TCP packet to port 80 on 11.22.33.44:80, where the TCP port is separated by a colon. Another important port is port 25 (SMTP) which is used for email. When an email to user@11.22.33.44 is to be delivered, a connection will made to 11.22.33.44:25.
Sometimes you don’t want to have so much transmission control overhead. Imagine that you are sending some voice data so you want to send as many packets (maybe use forward error correcting codes) but you don’t want to bother with retransmission of lost packets. The voice data simply isn’t useful if it is not delivered on time. In such cases we would prefer a more basic protocol which doesn’t isolate us from the unreliability of IP.
This protocol is called UDP and it is really barebones. UDP is basically IP with some added port numbers (and error detection checksums). From now on we can’t simply talk about “port 80″ on host but we must say whether we mean port 80 in the tcp protocol (TCP:80) or in the udp protocol (UDP#80).
Speaking of UDP ports, let me tell you about a really important one. The (206.190.36.45, 98.138.253.109, 98.139.183.24).” My browser will connect to one of these IPs (over HTTP = TCP:80) chosen at random.
Another useful UDP service is DHCP (dynamic host configuration protocol). This is the magical process by which you are automatically assigned an IP address when you join a network. DHCP bootstraps the communication (you joined a new network, ok, but what is the network number for this network? who should you talk to? What IP address should you respond to?). Either you know this information (someone gave it to you on a piece of paper [sysadmin]) or you can make a DHCP request (which is UDP broadcast) and a DHCP server will respond to you and assign you an IP address, tell you what the network number is and tell you which router to talk to to go towards the Internet (the route).
Ok so everyone knows the basics now, but HN doesn’t just give you the basics — it gives you the advanced stuff too. What are the current problems with TCP/IP?
advm says:
Maybe TCP’s issues aren’t apparent when you’re using it to download page assets from AWS over your home Internet connection, but they become apparent when you’re doing large file transfers between systems whose bandwidth-delay products (BDPs) greatly exceed the upper limit of the TCP buffers on the end systems.
This may not be an issue for users of consumer grade Internet service, but it is an issue to organizations who have private, dedicated, high-bandwidth links and need to move a lot of data over large distances (equating to high latency) very quickly and often; CDNs, data centers, research institutions, or, I dunno, maybe someone like Google.
The BDP and the TCP send buffer size impose an upper limit on the window size for the connection. Ideally, in a file transfer scenario, the BDP and the socket’s send buffer size should be equal. If your send buffer size is lower than the BDP, you cannot ever transfer at a greater throughput than buffer_size / link_latency, and thus you cannot ever attain maximum bandwidth. I can explain in more detail why that’s true if you want, but otherwise here’s this: http://www.psc.edu/index.php/networking/641-tcp-tune
Unfortunately for end systems with a high BDP between them, most of the time the maximum send buffer size for a socket is capped by the system to something much lower than the BDP. This is a result of the socket implementation of these systems, not an inherent limitation of TCP.
An accepted user-level solution to this issue is to use multiple sockets in parallel, but that has its own issues, such as breaking fairness and not working well with the stream model. I can explain this more if you want, too, just let me know.There are other problems with TCP, such as
slow start being, well, slow to converge on high-BDP networks,
bad performance in the face of random packet loss (e.g., TCP over Wi-Fi),
congestion control algorithms being too conservative (IMO, not everyone needs to agree on the same congestion control protocol for it to work well, it just needs to converge to network conditions faster, better differentiate types of loss, and yield to fairness more quickly),
TCP features such as selective ACKs not being widely used,
default TCP socket settings sucking and requiring a lot of tuning to get right,
crap with NAT that can’t be circumvented at the user level (UDP-based stream protocols can do rendezvous connections to get around NAT), and more.People write whole papers on all these things. Problem is most of the public research exists as a shitty academic papers you wouldn’t probably bother reading anyway, and most of the people actually studying this stuff in-depth and coming up with solutions are private researchers and engineers working for companies like Google.
The last paragraph is a good reason why there should be a “No BS guide to computer systems”. I bet I can show services at all layers of the OSI stack and really go into details. The sockets are pretty cool.
pjscott describes the crypto stack in just one sentence:
Their crypto stuff looks pretty reasonable. Key exchange uses ECDH with either the P-256 or curve25519 polynomials. Once the session key is established, it’s encrypted with AES-128 and authenticated with either GCM or HMAC-SHA256. None of this is implemented yet, but it’s at least cause for hope.
latitude also gives other considerations about doing crypto over the Internet.
I’ll tell you a dirty little secret of the protocol design.
Say, you want to design a protocol with reliable delivery and/or loss detection. You will then have ACKs, send window and retransmissions. Guess what? If you don’t follow windowing semantics of TCP, then one of two things will happen on saturated links – either TCP will end up with all the bandwidth or you will.
So – surprise! – you have no choice but to design a TCP clone.That said, there is a fundamental problem with TCP, when it’s used for carrying secure connections. Since TCP acts as a pure transport protocol, it has no per-packet authentication and so any connection can be trivially DoS’d with a single fake FIN or RST packet. There are ways to solve this, e.g. by reversing the TCP and security layers and running TCP over ESP-over-UDP or TLS-over-UDP (OpenVPN protocol). This requires either writing a user-space TCP library or doing some nasty tunneling at the kernel level, but even as cumbersome as this is, it’s still not a reason enough to re-invent the wheel. Also, if you want compression, it’s readily available in TLS or as a part of IPsec stack (IPcomp). If you want FEC, same thing – just add a custom transform to TLS and let the client and server negotiate if to use it or not.
I mean, every network programmer invents a protocol or two in his lifetime. It’s like a right of passage and it’s really not a big deal.
I learned stuff today. I hope you guys learned something too.
