I spent the last week drawing. More specifically, drawing in concept space. Drawing concept maps for the linear algebra book.

Without going into too much details, the context is that the old concept map was too overloaded with information, so I decided to redo it. I had to split the concept map on three pages, because there’s a lot of stuff to cover. Check it out.

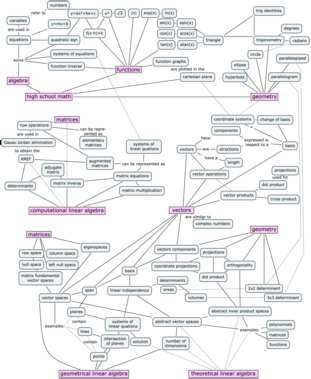
Math basics and how they relate to geometric and computational aspects of linear algebra

The skills from high school math you need to “import” to your study of linear algebra are geometry, functions, and the tricks for solving systems of equations (e.g. the values $x$ and $y$ that simultaneously satisfy the equations $x+y=3$ and $3x+y=5$ are $x=1$ and $y=2$.)

The first thing you’ll learn in linear algebra is the Gauss–Jordan elimination procedure, which is a systematic approach for solving systems of $n$ equations with $n$ unknowns. You’ll also learn how to compute matrix products, matrix determinants, and matrix inverses. This is all part of Chapter 3 in the book.

In Chapter 4, we’ll learn about vector spaces and subspaces. Specifically, we’ll discuss points in $\mathbb{R}^3$, lines in $\mathbb{R}^3$, planes in $\mathbb{R}^3$, and $\mathbb{R}^3$ itself. The basic computational skills you picked up in Chapter 3 can be used to solve interesting geometric problems in vectors spaces with any number of dimensions $\mathbb{R}^n$.

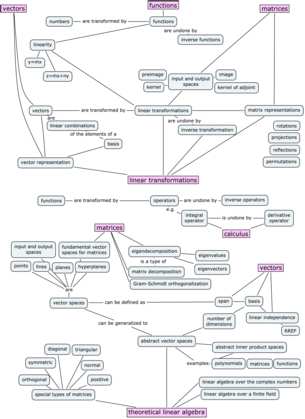
Linear transformations and theoretical topics

The concept of a linear transformation $T:\mathbb{R}^n \to \mathbb{R}^m$ is the extension of the idea of a function of a real variable $f:\mathbb{R} \to \mathbb{R}$. Linear transformations are linear functions that take $n$-vectors as inputs and produce $m$-vectors as outputs.

Understanding linear transformations is synonymous with understanding linear algebra. There are many properties of a linear transformation that we might want to study. The practical side of linear transformations is their nature as a vector-upgrade to your existing skill set of modelling the world with functions. You’ll also learn how to study, categorize, and understand linear transformations using new theoretical tools like eigenvalues and eigenvectors.

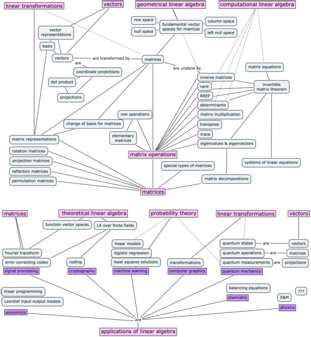
Matrices and applications

Another fundamental idea in linear algebra is the equivalence between linear transformations $T:\mathbb{R}^n \to \mathbb{R}^m$ and matrices $M \in \mathbb{R}^{m\times n}$. Specifically, the abstract idea of a linear transformation $T:\mathbb{R}^n \to \mathbb{R}^m$, when we fix a particular choice of basis $B_i$ for the input space and $B_o$ for the output space of $T$, can be represented as a matrix of coefficients $_{B_o}[M_T]_{B_i} \in \mathbb{R}^{m\times n}$. The precise mathematical term for this equivalence is isomorphism. The isomorphism between linear transformations and their matrix representations means we can characterize the properties of a linear transformation by analyzing its matrix representation.

Chapter 7 in the book contains a collection of short “applications essays” that describe how linear algebra is applied to various domains of science and business. Chapter 8 is a mini-intro to probability theory and Chapter 9 is an intro course on quantum mechanics. All the applications are completely optional, but I guarantee you’ll enjoy reading them. The power of linear algebra made manifest.

If you’re a seasoned blog reader, and you just finished reading this post, I know what you’re feeling… a moment of anxiety goes over you—is a popup asking you to sign up going to show up from somewhere, is there going to be a call to action of some sort?

Nope.