The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Functions reference
{{page>math:functions:&noheader&doindent}}
Line
Definition
The equation of a line consists of a multiple of $x$ plus some constant: \[ f(x) = mx+b. \]
Parameters
- $m$ is the slope.
- $b$ is the $y$-intercept. The value of the function when $x=0$.
- $b/m$ is the $x$-intercept. Another word for $x$-intercept is root, i.e., a value where $f(x)=0$.
Properties
- There is a unique linear function that passes through any two points $(x_1,y_1)$ and $(x_2,y_2)$ if $x_1 \neq x_2$.
- The inverse function of $f(x)=\frac{1}{m}(x-b)$.
Graph
Here is the graph of \[ f(x) = 2x - 3. \]
A line can also be described in a more symmetric form. \[ Ax + By = C, \] This is known as the general equation of a line. We have $b=\frac{C}{B}$ and $m=\frac{-A}{B}$.
Square
The square function is also known as the quadratic function, the second degree function, or simply called a parabola.
Definition
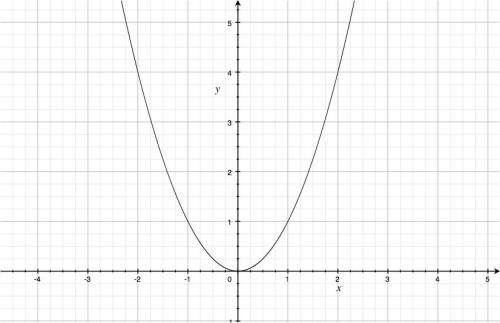
The bare quadratic function has the form: \[ f(x)=x^2. \]
Properties
- Inverse of $\sqrt{x}$.
- Never negative: $x^2 \geq 0$, for all $x\in \mathbb{R}$.
- The quadratic function is two-to-one since it sends both $x$ and $-x$ to $x^2=(-x)^2$.
- The quadratic function is convex, i.e., it curves upwards.
Square root
Definition
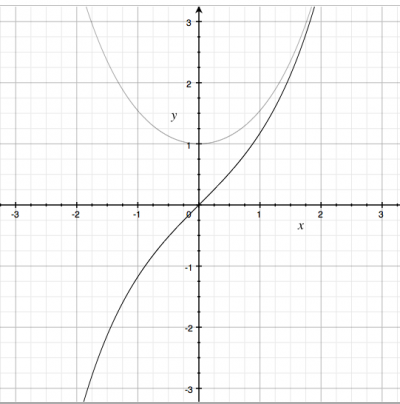
The function returns a number $y$ such that $y^2=x$: \[ f(x) = \sqrt{x} \equiv x^{\frac{1}{2}} . \]
Graph
The graph of the square root function looks like this:
{{ :math:sqrt_of_x.jpg?500 |The graph of the function $\sqrt{x}$.}}
Properties
- The inverse of $x^2$.
- Since there is no real number $y$ such that
$y^2$ is negative, the function $f(x)=\sqrt{x}$
is not defined for negative inputs $x$.
Parameters
- $2$: the degree of the root operation. More generally
you can have $n$th root $\sqrt[n]{x}$ which is the inverse
function to $x^n$. For example, the inverse function for the
cubic function $f(x)=x^3$ is the //cube root//:
\[
f(x) = \sqrt[3]{x} \equiv x^{\frac{1}{3}}.
\]
So we have $\sqrt[3]{8}=2$ since $2\times2\times2=8$.
Absolute value
The $\textrm{abs}$ function is used when you need to get the size of a number and you don't care if the number is positive or negative. The absolute value just ignores the sign of a number.
Definition
\[ f(x)=|x|= x \text{ if } x>0 \text{ or } -x \text{ if } x<0 \]
Properties
- Always returns a non-negative number.
- The combination of squaring followed by square-root is equivalent
to the absolute value function:
\[
\sqrt{ x^2 } \equiv |x|.
\]
Sine
Contrary to what religious leaders might lead you to believe, there is nothing wrong with $\sin$. At least not with the mathematical $\sin$. The sinus, sine or $\sin$ function tells you the ratio of the lengths of two sides in a right angle triangle.
Definition
Let us not talk about triangles, angles and lengths of sides for now, but think of the $\sin$ function as a generic function of $x$: \[ f(x)=\sin(x). \]
Properties
- The $\sin$ function is odd, which the mathematical term for saying:
\[ f(-x) = -f(x). \]
- The function is periodic, with period $2\pi$, that is:
\[ f(x) = f(x+2\pi). \]
- Relation to $\cos$: $\sin^2 x + \cos^2 x = 1$.
- Relation to $\csc$: $\csc(x) \equiv \frac{1}{\sin x}$ ($\csc$ is read cosecant).
- The inverse function is $\sin^{-1}(x)=\arcsin(x)$, and is not
to be confused with $(\sin(x))^{-1}=\frac{1}{\sin(x)} \equiv \csc(x)$.
Graph
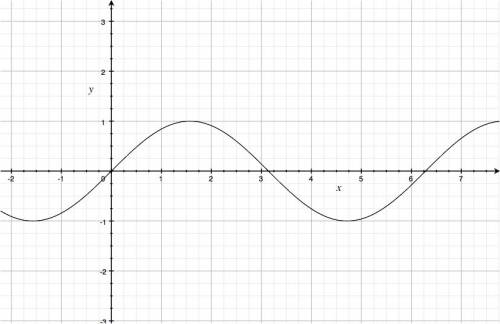
The function starts from zero $\sin(0)=0$, then goes up to take on the value $1$ at $x=\frac{\pi}{4}$, then falls down until it crosses the $x$ axis at $x=\pi$.
After $\pi$ the function drops below the $x$ axis and reaches its minimum value of $-1$ at $x=\frac{3\pi}{2}$ only to come up again and repeat the $2\pi$-long cycle starting from $x=2\pi$.
We have $0=\sin(0)=\sin(\pi)=\sin(2\pi)=\sin(3\pi)=\cdots$, in fact $\sin(x)$ has a root at each multiples of $\pi$.
Cosine
Definition
\[ f(x)=\cos(x). \]
Graph
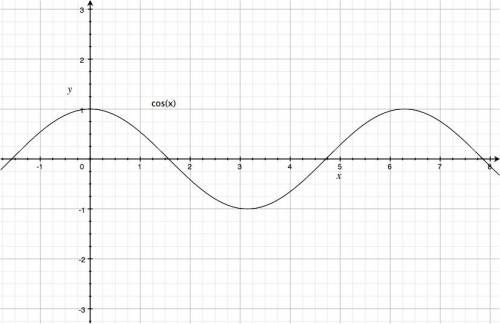
Cos starts off from $\cos(0)=1$ and then drops down to cross the $x$ axis at $x=\frac{\pi}{2}$. Cos then continues until it reaches its minimum value at $x=\pi$. The function then comes back up, crosses the $x$ axis again at $x=\frac{3\pi}{2}$, and goes back up to its maximum value at $x=2\pi$.
Properties
- The $\cos$ function is even, which means it doesn't care
about the sign of the input:
\[
\cos(-x) = \cos(x).
\]
* The cosine function is a shifted version of the sine function
\[
\cos(x) = \sin(x+\frac{\pi}{2}).
\]
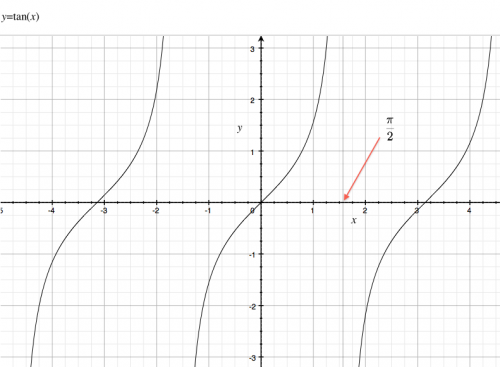
Tangent
Definition
\[ f(x)=\tan(x)\equiv \frac{ \sin(x) } { \cos(x) }. \]
Graph
Properties
- The function $\tan$ is periodic with period $\pi$, not $2\pi$ like $\sin$ and $\cos$.
- The $\tan$ function has asymptotes at all values of $x$ for which the denominator ($\cos$) goes to zero.
- The locations of the asymptotes are $x=\frac{\pi}{2},\frac{-\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\ldots$.
- At those values, $\tan$ approaches $\infty$ from the left, and $-\infty$ from the right.
- Value at $0$: $\tan(0)=\frac{0}{1}=0$ because $\sin(0)=0$.
- The angle $x=\frac{\pi}{4}$ is special since both $\sin$ and $\cos$ are equal
and we get:
\[
\tan\left(\frac{\pi}{4} \right)
= \frac{ \sin\left(\frac{\pi}{4}\right) }{ \cos\left(\frac{\pi}{4}\right) }
= \frac{ \frac{\sqrt{2}}{2} }{ \frac{\sqrt{2}}{2} }
= 1.
\]
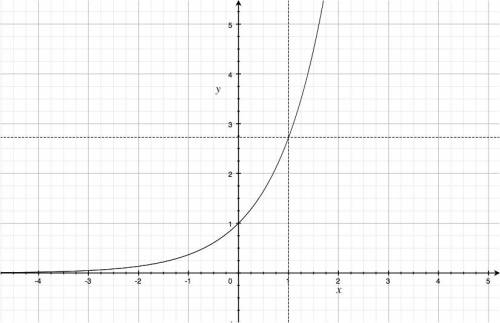
Exponential
Definition
\[ f(x)=Ae^{\gamma x}. \]
Graph
The exponential function graph:
Parameters
- $A$: the initial value, $A=f(0)$. The graph shows the case $A=1$.
- $\gamma$: the rate of the exponential.
For $\gamma > 0$ the function is increasing.
for $\gamma < 0$ the function is decreasing
and tends to zero for large values of $x$.
The case $\gamma=0$ is special since $e^{0}=1$,
and so the exponential becomes the constant function $f(x)=A$.
The graph shows the case $\gamma=1$.
Properties
- The number $e$ is related to the following limit argument
\[ e = \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n, \]
which can be interpreted as a formula for compounding interest.
The limit as $n$ goes to infinity refers to a scenario when
the compounding is performed infinitely often.
* The derivative (slope) of the exponential function is
equal to the exponential function:
\[
f(x) = e^x \ \ \Rightarrow \ \ f'(x)=e^x.
\]
In function $e^x$ is equal to its derivative: $f(x)=f'(x)$.
Links
[ the exponential function $2^x$ for the naturals $x \in \mathbb{N}$ can easily be evaluated by drawing ]
http://www.youtube.com/watch?v=e4MSN6IImpI
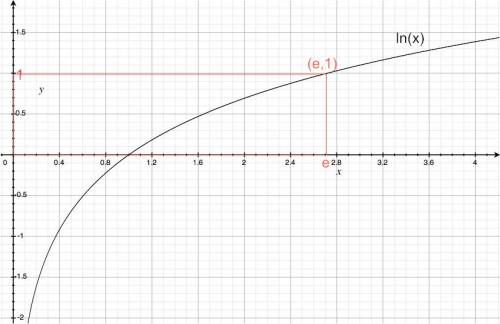
Natural logarithm
Definition
\[ f(x)=\ln(x) = \log_e(x). \]
Graph
The natural logarithm function:
Parameters
- $e$: the natural logarithm is the logarithm base $e$.
Properties
- Inverse of the exponential function $e^x$.
Polynomials
Definition
\[ f(x)=a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots + a_nx^n, \] where the $a_i$s are the coefficients.
Parameters
- $n$: the degree of the polynomial. A polynomial of degree $n$ has $n+1$ coefficients $a_i$.
- $a_0$: the constant term.
- $a_1$: the linear coefficient, or first order coefficient.
- $a_2$: the quadratic coefficient.
- $a_3$: the cubic coefficient.
- $a_n$: the $n$th order coefficient.
Properties
- The sum of two polynomials is also a polynomial.
Function transformations
It is often required to adjust the shape of a function by scaling to it or moving it so as to make it pass through certain points. For example, if we wanted to have a function $g$ with the same shape as the absolute value function $f(x)=|x|$, but for which $g(0)=3$, we would use the function $g(x)=|x|+3$.
In this section, we will discuss the four basic transformations you can do on any function $f$ to obtain a transformed function $g$:
- Vertical translation: $g(x) = f(x)+k$.
- Horizontal translation: $g(x) = f(x-h)$.
- Vertical scaling: $g(x) = Af(x)$.
- Horizontal scaling: $g(x) = f(ax)$.
By using these transformations we can move and
stretch a generic function to give it any desired
shape.
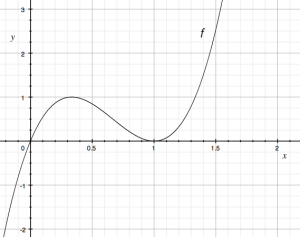We will illustrate all of the above transformations
on the following function:
\[
f(x) = 6.75(x^3 - 2x^2 +x).
\]
This function is chosen because it has distinctive features
in both the horizontal and vertical directions.
By observing the graph of this function, we see that its
$x$-intercepts are at $x=0$ and $x=1$.
The function $f$ also has a local maximum at $x=\frac{1}{3}$
and the height of the function there is $f(\frac{1}{3})=1$.
We can confirm the first observation mathematically by factoring the function as follows: \[ f(x) = 6.75x(x^2 - 2x +1) = 6.75x(x-1)^2, \] where we see clearly that $f(x)=0$ if $x=0$ (the $x$ factor kills it) or $x=1$ (the $(x-1)$ factor kills it).
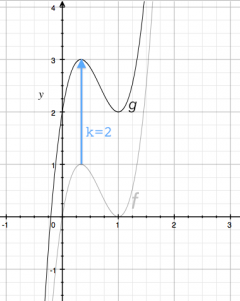
Vertical translations
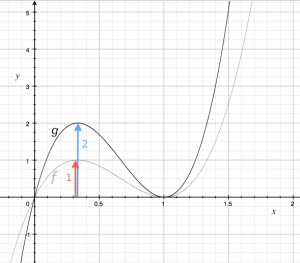
If we want to move a function $f$ up by $k$ units, we simply add $k$ to the function: \[ g(x) = f(x) + k. \] The function $g(x)$ will have exactly the same shape as $f(x)$ but it will be translated (the mathematical term for moved) upwards by $k$ units.
Recall the function $f(x) = 6.75(x^3 - 2x^2 +x)$. If we wanted to move the function up by $k=2$ units, we would obtain: \[ g(x) = f(x)+2 = 6.75(x^3 - 2x^2 +x) + 2, \] and the graph of $g(x)$ will be as shown on the right. The original function $f(x)$ crossed the $x$-axis at $x=0$, so we had $f(0)=0$. The transformed function must therefore obey $g(0)=2$. The maximum at $x=\frac{1}{3}$ has similarly shifted in value from $f(\frac{1}{3})=1$ to $g(\frac{1}{3})=3$.
Horizontal translation
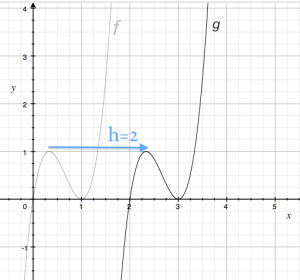
We can move a function $f$ to the right by $h$ units by subtracting $h$ from $x$ and using that as the input argument: \[ g(x) = f(x-h). \] The point $(0,f(0))$ on $f(x)$ will now correspond to the point $(h,g(h))$ on $g(x)$.
Consider the graph on the right which shows the function $f(x)= 6.75(x^3 - 2x^2 +x)$ as well as the function $g(x)$ which is shifted to the right by $h=2$ units: \[ g(x) = f(x-2) = 6.75\left[ (x-2)^3 - 2(x-2)^2 +(x-2) \right]. \]
The original function $f$ had $f(0)=0$ and $f(1)=0$ so the new function $g(x)$ must have $g(2)=0$ and $g(3)=0$. The maximum at $x=\frac{1}{3}$ has similarly shifted by two units to the right $g(2+\frac{1}{3})=1$.
Vertical scaling
To stretch or compress the shape of a function vertically, we can multiply it by some constant $A$ and obtain: \[ g(x) = Af(x). \] If $|A|>1$, the function will be stretched, and if $|A|<1$ the function will be compressed. If $A$ is negative, the function will also be flipped upside down (reflection through the $x$-axis).
There is an important difference between vertical translation and vertical scaling. Translation moves all the points of the function the same amount, whereas scaling moves each point proportionally to how far it is from the $x$ axis.
On the right, we see the graph on the function $f(x)= 6.75(x^3 - 2x^2 +x)$ and the function $g(x)$ which is equal to $f(x)$ stretched vertically by a factor of $A=2$: \[ g(x) = 2f(x) = 13.5(x^3 - 2x^2 +x). \]
The $x$-intercepts $f(0)=0$ and $f(1)=0$ didn't move: $g(0)=0$ and $g(1)=0$. The maximum at $x=\frac{1}{3}$ has now doubled in value $g(\frac{1}{3})=2$. Indeed, all values of $f(x)$ have been stretched upwards by a factor of 2, as can be verified with the point $f(1.5)=2.5$ which has become $g(1.5)=5$.
Horizontal scaling
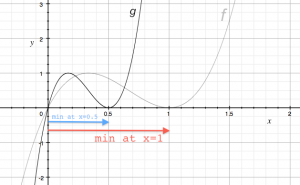
To stretch or compress a function horizontally we can multiply the input value by some constant $a$ to obtain: \[ g(x) = f(ax). \] If $|a|>1$, the function will be compressed, and if $|a|<1$ the function will be stretched. Note that the behaviour here is the opposite of the vertical case. If $a$ is a negative number, the function will also be flipped horizontally (reflection through the $y$-axis).
The graph on the right shows the function $f(x)= 6.75(x^3 - 2x^2 +x)$ and the function $g(x)$ which is $f(x)$ compressed horizontally by a factor of $a=2$: \[ g(x) = f(2x) =6.75\left[ (2x)^3 - 2(2x)^2 +(2x)\right]. \]
The $x$-intercept $f(0)=0$ didn't move since it is on the $y$-axis. The $x$-intercept $f(1)=0$ did move however and we now have $g(0.5)=0$. The maximum at $x=\frac{1}{3}$ has now moved to $g(\frac{1}{6})=1$. All values of $f(x)$ have been compressed towards the $y$-axis by a factor of 2.
General quadratic function
Definition
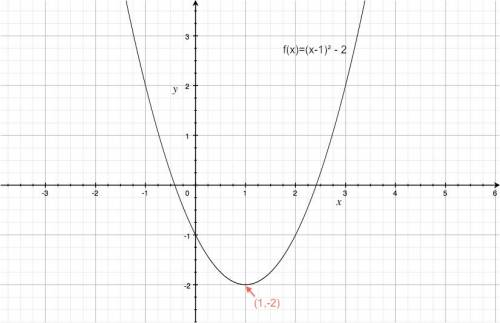
The general quadratic function has the following form: \[ f(x) = A(x-h)^2 + k, \] where $x$ is the input and $A,h$ and $k$ are the parameters.
Parameters
- $A$: slope multiplier.
- The larger the value of $A$ the steeper the slope.
- If $A<0$ (negative), then the function opens downwards.
- $h$: horizontal displacement of the function centre. Notice that subtracting a
number inside the bracket $(\ )^2$ (i.e. positive $h$) makes the function go to the right.
- $k$: vertical displacement of the function.
If a quadratic crosses the $x$-axis, then it can be written in factored form \[ f(x) = (x-a)(x-b), \] where $a$ and $b$ are the two roots.
Another very common way of writing a quadratic function is \[ f(x) = Ax^2 + Bx + C. \]
Properties
- There is a unique parabola that passes through any three points $(x_1,y_1),$ $(x_2,y_2)$ and $(x_3,y_3)$ if
the points have different $x$ coordinates $x_1 \neq x_2$, $x_2 \neq x_3$ and $x_1 \neq x_3$.
- The derivative of $f(x)=Ax^2 + Bx + C$ is $f'(x)=2Ax + B$.
Graph
When $h=1$ (one unit shifted to the right) and $k=-2$ (two units shifted downwards), we get the following graph:
General sin function
Parameters
Introducing all possible parameters into the sine function we get: \[ f(x) = A\sin( kx - \phi), \] where $A$, $k$ and $\phi$ are the parameters.
- $A$ is the amplitude, which tells you the distance the function will go above and below the $x$ axis as it oscillates.
- $k$ is the wave number and decides how many times the graph goes up and down within one period of $2\pi$. For the “bare” sine, $k=1$ and the function makes one cycle as $x$ goes from $0$ to $2\pi$. If $k=2$ the function will go up and down twice.
- $\phi$ is a phase shift, analogous to the horizontal shift $h$ which we have seen. This is a number which dictates where the oscillation starts. The default sine function has zero phase shift ($\phi=0$), so it starts from zero with an increasing slope.
Instead of counting how many times the function goes up and down, we can instead talk about the wavelength of the function: \[ \lambda \equiv \text{ wavelength} = \{ \text{ the distance form one peak to the next } \}. \] The “bare” sine has wavelength $2\pi$, but when we introduce some wave number multiplier $k$, the wavelength becomes: \[ \lambda = \frac{2\pi}{k}. \]
Hyperbolic cos and sin
If we follow the $x$ and $y$ coordinates of a point $P$ that is on the unit circle, we will see that the $x=\cos(\theta)$ and $y=\sin(\theta)$, where $\theta$ is the angle of the point. This is called circular trigonometry.
We can also have hyperbolic trigonometry, if we replace the circle with a hyperbola. The $x$-coordinate of a point $Q$ that traces out the shape of a hyperbola will have the formula $\cosh$ and its $y$ coordinate will be $\sinh$.
Definition
We can define the hyperbolic functions in terms of the exponential function: \[ \cosh x = \frac{e^{x} + e^{-x}}{2}, \qquad \sinh x = \frac{e^{x} - e^{-x}}{2}. \]
Graph
Parameters
Properties
- $\cosh$ is an even function, while $\sinh$ is odd.
In fact you can think of $\cosh x$ as the “even part of $e^x$,
and $\sinh x$ as the odd part of $e^x$ since \[ e^x = \cosh x + \sinh x. \]
The equivalent of the circular-trigonometric identity $\cos^2 \theta + \sin^2 \theta = 1$, is the following: \[ \cosh^2 x - \sinh^2 x = 1. \]
Applications
A long wire suspended between two lamp posts will sag in the middle producing a curved shape. The exact equation that describes the shape of the cable is the hyperbolic cosine function: $\cosh x$.