The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Introduction
One of the coolest things about understanding math is that you will automatically start to understand the laws of physics too. Indeed, most physics laws are expressed as mathematical equations. If you know how to manipulate equations and you know how to solve for the unknowns in them, then you know half of physics already.
Ever since Newton figured out the whole $F=ma$ thing, people have used mechanics in order to achieve great technological feats like landing space ships on The Moon and recently even on Mars. You can be part of that too. Learning physics will give you the following superpowers:
- The power to predict the future motion of objects using equations.
It is possible to write down the equation which describes the position of
an object as a function of time $x(t)$ for most types of motion.
You can use this equation to predict the motion at all times $t$,
including the future.
"Yo G! Where's the particle going to be at when $t=1.3$[s]?",
you are asked. "It is going to be at $x(1.3)$[m] bro."
Simple as that. If you know the equation of motion $x(t)$,
which describes the position for //all// times $t$,
then you just have to plug $t=1.3$[s] into $x(t)$
to find where the object will be at that time.
- Special **physics vision** for seeing the world.
You will start to think in term of concepts like force, acceleration and velocity
and use these concepts to precisely describe all aspects of the motion of objects.
Without physics vision, when you throw a ball in the air you will see it go up,
reach the top, then fall down.
Not very exciting.
Now //with// physics vision,
you will see that at $t=0$[s] a ball is thrown into the $+\hat{y}$ direction
with an initial velocity of $\vec{v}_i=12\hat{y}$[m/s]. The ball reaches a maximum
height of $\max\{ y(t)\}= \frac{12^2}{2\times 9.81}=7.3$[m] at $t=12/9.81=1.22$[s],
and then falls back down to the ground after a total flight time of
$t_{f}=2\sqrt{\frac{2 \times 7.3}{9.81}}=2.44$[s].
Why learn physics?
A lot of knowledge buzz awaits you in learning about the concepts of physics and understanding how the concepts are connected. You will learn how to calculate the motion of objects, how to predict the outcomes of collisions, how to describe oscillations and many other things. Once you develop your physics skills, you will be able to use the equations of physics to derive one number (say the maximum height) from another number (say the initial velocity of the ball). Physics is a bit like playing LEGO with a bunch of cool scientific building blocks.
By learning how to solve equations and how to deal with complicated physics problems, you will develop your analytical skills. Later on, you can apply these skills to other areas of life; even if you do not go on to study science, the expertise you develop in solving physics problems will help you deal with complicated problems in general. Companies like to hire physicists even for positions unrelated to physics: they feel confident that if the candidate has managed to get through a physics degree then they can figure out all the business shit easily.
Intro to science
Perhaps the most important reason why you should learn physics is because it represents the golden standard for the scientific method. First of all, physics deals only with concrete things which can be measured. There are no feelings and zero subjectivity in physics. Physicists must derive mathematical models which accurately describe and predict the outcomes of experiments. Above all, we can test the validity of the physical models by running experiments and comparing the outcome predicted by the theory with what actually happens in the lab.
The key ingredient in scientific thinking is skepticism. The scientist has to convince his peers that his equation is true without a doubt. The peers shouldn't need to trust the scientist, but instead carry out their own tests to see if the equation accurately predicts what happens in the real world. For example, let's say that I claim that the equation of motion for the ball thrown up in the air with speed $12$[m/s] is given by $y_c(t)=\frac{1}{2}(-9.81)t^2 + 12t+0$. To test whether this equation is true, you can perform the throwing-the-ball-in-the-air experiment and record the maximum height the ball reaches and the total time of flight and compare them with those predicted by the claimed equation~$y_c(t)$. The maximum height that the ball will attain predicted by the claimed equation occurs at $t=1.22$ and is obtained by substituting this time into the equation of motion $\max_t\{ y_c(t)\}=y_{c}(1.22)=7.3$[m]. If this height matches what you measured in the real world, you can maybe start to trust my equation a little bit. You can also check whether the equation $y_c(t)$ correctly predicts the total time of flight which you measured to be $t=2.44$[s]. To do this you have to check whether $y_c(2.44) = 0$ as it should be when the ball hits the ground. If both predictions of the equation $y_c(t)$ match what happens in the lab, you can start to believe that the claimed equation of motion $y_c(t)$ really is a good model for the real world.
The scientific method depends on this interplay between experiment and theory. Theoreticians prove theorems and derive physics equations, while experimentalists test the validity of the equations. The equations that accurately predict the laws of nature are kept while inaccurate models are rejected.
Equations of physics
The best of the equations of physics are collected and explained in textbooks. Physics textbooks contain only equations that have been extensively tested and are believed to be true. Good physics textbooks also show how the equations are derived from first principles. This is really important, because it is much easier to remember a few general principles at the foundation of physics rather than a long list of formulas. Understanding trumps memorization any day of the week.
In the next section we learn about the equations $x(t)$, $v(t)$ and $a(t)$ which describes the motion of objects. We will also illustrate how the position equation $x(t)=\frac{1}{2}at^2 + v_it+x_i$ can be derived using simple mathematical methods (calculus). Technically speaking, you are not required to know how to derive the equations of physics—you just have to know how to use them. However, learning a bit of theory is a really good deal: reading a few extra pages of theory will give you a deep understanding of, not one, not two, but eight equations of physics.
Physics fundamentals
We begin with a lightning fast introduction to the basic tools of physics.
Mathematical methods
If you read chapter one of this book, you are now optimally prepared to learn physics. You are not afraid of numbers or simple algebra rules. You know how to solve equations. You are familiar with functions such as the linear function $f(x)=mx+b$ and the quadratic function $f(x)=ax^2+bx+c$. In particular you should know how to solve the quadratic equation. Sometimes there will be two unknowns to solve for in a physics problem, but this is not much harder. If you have two equations that you know to be true, then you can solve two equations simultaneously to find both unknowns.
Vectors
Most of the cool quantities in physics are vectors $\vec{v}=(v_x,v_y)$. Velocity is a vector, forces are vectors, and the electric and magnetic fields are vectors too. Dealing with vectors involves dealing with their components. So saying that $\vec{a}=\vec{b}$ is really saying that the $x$ components of these vectors are equal \[ a_x = b_x, \] and their $y$ components are equal too: \[ a_y = b_y. \] So when I say that $\vec{v}_i = 0\hat{x} + 12\hat{y}$, I am saying that the $x$-component is zero $v_{ix} = 0$ and the $y$-component is twelve $v_{iy}= 12$. However, the teacher won't make physics easy for you on the homework, and definitely not on the exams. He or she won't tell you the vector components, but instead say something like “the initial velocity $\vec{v}_i$ is 12[m/s] and it acts at an angle of 90 degrees with respect to the $x$ axis.” This is the length-and-direction way of talking about vectors. To get the $x$ and $y$ components of the vector $\vec{v}_i$ you have to use cos and sin as follows: \[ v_{ix} = 12 \cos 90=0, \qquad v_{iy} = 12 \sin 90=12. \] If this doesn't seem obvious to you, then you should draw a right-angle triangle and recall the definitions of sin and cos.
We will discuss vectors in more depth in Chapter 3.
Calculus
Yes, calculus. You need to understand calculus in order to understand mechanics properly. The two subjects are meant for each other. This is in fact the whole idea behind this book.
It is possible to teach physics without calculus. For example, a teacher could state the equations of kinematics (the area of physics which deals with the motion of objects) without proof. This “memorize the equations” approach is how physics is usually taught in high school. The equations are true “by revelation”. This is an OK way to learn physics when you are in high school, because the only mathematical technique you know as a kid is how to solve equations. Indeed just knowing how to use the equations of kinematics is quite enough to solve many physics problems.
Later on in this chapter (after learning a bit about calculus), we will revisit the equations of kinematics and see where they actually come from. You are adults now. You can handle the truth. Don't worry though, it won't take more than a couple of pages.
Kinematics
Kinematics (from the Greek word kinema for motion) is the study of trajectories of moving objects. The equations of kinematics can be used to calculate how long a ball thrown upwards will stay in the air, or to calculate the acceleration needed to go from 0 to 100 km/h in 5 seconds. To carry out these calculations we need to know which equation of motion to use and the initial conditions (the initial position $x_i$ and the initial velocity $v_{i}$). Plug in the knowns into the equations of motion and then you can solve for the desired unknown using one or two simple algebra steps. This entire section boils down to three equations. It is all about the plug-number-into-equation technique.
The purpose of this section is to make sure that you know how to use the equations of motion and understand concepts like velocity and accretion well. You will also learn how to easily recognize which equation is appropriate need to use to solve any given physics problem.
Concepts
The key notions used to describe the motion of an objects are:
- $t$: the time, measured in seconds [s].
- $x(t)$: the position of an object as a function of time—also known as the equation of motion. The position of an object is measured in metres [m].
- $v(t)$: the velocity of the object as a function of time. Measured in [m/s].
- $a(t)$: the acceleration of the object as a function of time. Measured in [m/s$^2$].
- $x_i=x(0), v_i=v(0)$: the initial (at $t=0$) position and velocity of the object (initial conditions).
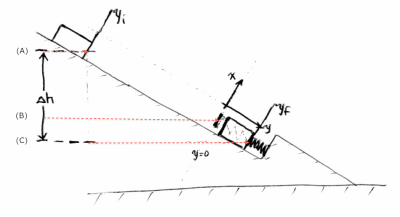
Position, velocity and acceleration
The motion of an object is characterized by three functions: the position function $x(t)$, the velocity function $v(t)$ and the acceleration function $a(t)$. The functions $x(t)$, $v(t)$ and $a(t)$ are connected—they all describe different aspects of the same motion.
You are already familiar with these notions from your experience driving a car. The equation of motion $x(t)$ describes the position of the car as a function of time. The velocity describes the change in the position of the car, or mathematically \[ v(t) \equiv \text{rate of change in } x(t). \] If we measure $x$ in metres [m] and time $t$ in seconds [s], then the units of $v(t)$ will be metres per second [m/s]. For example, an object moving at a constant speed of $30$[m/s] will have its position change by $30$[m] each second.
The rate of change of the velocity is called the acceleration: \[ a(t) \equiv \text{rate of change in } v(t). \] Acceleration is measured in metres per second squared [m/s$^2$]. A constant positive acceleration means the velocity of the motion is steadily increasing, like when you press the gas pedal. A constant negative acceleration means the velocity is steadily decreasing, like when you press the brake pedal.
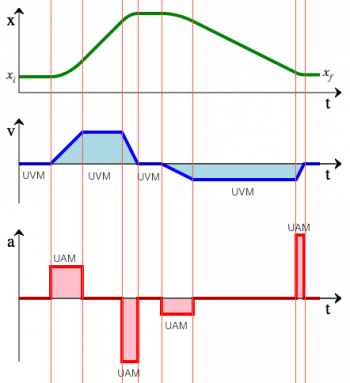 The illustration on the right shows the simultaneous graph of the
position, velocity and acceleration of a car during some time interval.
In a couple of paragraphs, we will discuss the exact mathematical equations which
describe $x(t)$, $v(t)$ and $a(t)$. But before we get to the math,
let us visually analyze the motion illustrated on the right.
The illustration on the right shows the simultaneous graph of the
position, velocity and acceleration of a car during some time interval.
In a couple of paragraphs, we will discuss the exact mathematical equations which
describe $x(t)$, $v(t)$ and $a(t)$. But before we get to the math,
let us visually analyze the motion illustrated on the right.
The car starts off with an initial position $x_i$ and just sits there for some time. The driver then floors the pedal to produce a maximum acceleration for some time, picks up speed and then releases the accelerator, but keeps it pressed enough to maintain a constant speed. Suddenly the driver sees a police vehicle in the distance and slams on the brakes (negative acceleration) and shortly afterwards brings the car to a stop. The driver waits for a few seconds to make sure the cops have passed. The car then accelerates backwards for a bit (reverse gear) and then maintains a constant backwards speed for an extended period of time. Note how “moving backwards” corresponds to negative velocity. In the end the driver slams on the brakes again to bring the car to a stop. The final position is $x_f$.
In the above example, we can observe two distinct types of motion. Motion at a constant velocity (uniform velocity motion, UVM) and motion with constant acceleration (uniform acceleration motion, UAM). Of course, there could be many other types of motion, but for the purpose of this section you are only responsible for these two.
- UVM: During times when there is no acceleration,
the car maintains a uniform velocity, that is,
$v(t)$ will be a constant function.
Constant velocity means that the position function
will be a line with a constant slope because, by definition, $v(t)= \text{slope of } x(t)$.
* UAM: During times where the car experiences a constant acceleration $a(t)=a$,
the velocity of the function will change at a constant rate.
The rate of change of the velocity is constant $a=\text{slope of } v(t)$,
so the velocity function must look like a line with slope $a$.
The position function $x(t)$ has a curved shape (quadratic) during moments of
constant acceleration.
Formulas
There are basically four equations that you need to know for this entire section. Together, these three equations fully describe all aspects of any motion with constant acceleration.
Uniform acceleration motion (UAM)
If the object undergoes a constant acceleration $a(t)=a$, like your car if you floor the accelerator, then its motion will be described by the following equations: \[ \begin{align*} x(t) &= \frac{1}{2}at^2 + v_i t + x_i, \nl v(t) &= at + v_i, \nl a(t) &= a, \end{align*} \] where $v_i$ is the initial velocity of the object and $x_i$ is its initial position.
There is also another useful equation to remember: \[ [v(t)]^2 = v_i^2 + 2a[x(t)- x_i], \] which is usually written \[ v_f^2 = v_i^2 + 2a\Delta x, \] where $v_f$ denotes the final velocity and $\Delta x$ denotes the change in the $x$ coordinate.
That is it. Memorize these equations, plug-in the right numbers, and you can solve any kinematics problem humanly imaginable. Chapter done.
Uniform velocity motion (UVM)
The special case where there is zero acceleration ($a=0$), is called uniform velocity motion or UVM. The velocity stays uniform (constant) because there is no acceleration. The following three equations describe the motion of the object under uniform velocity: \[ \begin{align} x(t) &= v_it + x_i, \nl v(t) &= v_i, \nl a(t) &= 0. \end{align} \] As you can see, these are really the same equations as in the UAM case above, but because $a=0$, some terms are missing.
Free fall
We say that an object is in free fall if the only force acting on it is the force of gravity. On the surface of the earth, the force of gravity produces a constant acceleration of $a=-9.81$[m/s$^2$]. The negative sign is there because the gravitational acceleration is directed downwards, and we assume that the $y$ axis points upwards. The motion of an object in free fall is described by the UAM equations.
Examples
We will now illustrate how the equations of kinematics are used to solve physics problems.
Moroccan example
Suppose your friend wants to send you a ball wrapped in aluminum foil from his balcony, which is located at a height of $x_i=44.145$[m]. How long does it take for the ball to hit the ground?
We recognize that this is a problem with acceleration, so we start by writing out the general UAM equations: \[ \begin{align*} y(t) &= \frac{1}{2}at^2 + v_i t + y_i, \nl v(t) &= at + v_i. \end{align*} \] To find the answer, we substitute the known values $y(0)=y_i=44.145$[m], $a=-9.81$ and $v_i=0$[m/s] (since the ball was released from rest) and solve for $t_{fall}$ in the equation $y(t_{fall}) = 0$ since we are interested in the time when the ball will reach a heigh of zero. The equation is \[ y(t_{fall}) = 0 = \frac{1}{2}(-9.81)(t_{fall})^2+0(t_{fall}) + 44.145, \] which has solution $t_{fall} = \sqrt{\frac{44.145\times 2}{9.81}}= 3$[s].
0 to 100 in 5 seconds
Suppose you want to be able to go from $0$ to $100$[km/h] in $5$ seconds with your car. How much acceleration does your engine need to produce, assuming it produces a constant amount of acceleration.
We can calculate the necessary $a$ by plugging the required values into the velocity equation for UAM: \[ v(t) = at + v_i. \] Before we get to that, we need to convert the velocity in [km/h] to velocity in [m/s]: $100$[km/h] $=\frac{100 [\textrm{km}]}{1 [\textrm{h}]} \cdot\frac{1000[\textrm{m}]}{1[\textrm{km}]} \cdot\frac{1[\textrm{h}]}{3600[\textrm{s}]}$= 27.8 [m/s]. We fill in the equation with all the desired values $v(5)=27.8$[m/s], $v_i=0$, and $t=5$[s] and solve for $a$: \[ v(5) = 27.8 = a(5) + 0. \] We conclude that your engine has to produce a constant acceleration of $a=5.56$[m/s$^2$] or more.
Moroccan example II
Some time later, your friend wants to send you another aluminum ball from his apartment located on the 14th floor (height of $44.145$[m]). In order to decrease the time of flight, he throws the ball straight down with an initial velocity of $10$[m/s]. How long does it take before the ball hits the ground?
Imagine the building with the $y$ axis measuring distance upwards starting from the ground floor. We know that the balcony is located at a height of $y_i=44.145$[m], and that at $t=0$[s] the ball starts with $v_i=-10$[m/s]. The initial velocity is negative, because it points in the opposite direction to the $y$ axis. We know that there is an acceleration due to gravity of $a_y=-g=-9.81$[m/s$^2$].
We start by writing out the general UAM equation: \[ y(t) = \frac{1}{2}a_yt^2 + v_i t + y_i. \] We want to find the time when the ball will hit the ground, so $y(t)=0$. To find $t$, we plug in all the known values into the general equation: \[ y(t) = 0 = \frac{1}{2}(-9.81)t^2 -10 t + 44.145, \] which is a quadratic equation in $t$. First rewrite the quadratic equation into the standard form: \[ 0 = \underbrace{4.905}_a t^2 + \underbrace{10.0}_b \ t - \underbrace{44.145}_c, \] and then solve using the quadratic equation: \[ t_{fall} = \frac{-b \pm \sqrt{ b^2 - 4ac }}{2a} = \frac{-10 \pm \sqrt{ 25 + 866.12}}{9.81} = 2.53 \text{ [s]}. \] We ignored the negative-time solution because it corresponds to a time in the past. Comparing with the first Moroccan example, we see that the answer makes sense—throwing a ball downwards will make it fall to the ground faster than just dropping it.
Discussion
Most kinematics problems you will be asked to solve follow the same pattern as the above examples. You will be given some of the initial values and asked to solve some unknown quantity. It is important to keep in mind the signs of the numbers you plug into the equations. You should always draw the coordinate system and indicate clearly (to yourself) the $x$ axis which measures the displacement. If a velocity or acceleration quantity points in the same direction as the $x$ axis then it is a positive number while quantities that point in the opposite direction are negative numbers.
All this talk of $v(t)$ being the “rate of change of $x(t)$” is starting to get on my nerves. The expression “rate of change of” is an euphemism for the calculus term derivative. We will now take a short excursion into the land of calculus in order to define some basic concepts (derivatives and integrals) so that we can use us this more precise terminology in the remainder of the book.
Projectile motion
Ever since the invention of gun powder, generation after generation of men have thought of countless different ways of hurtling shrapnel and explosives at each other. Indeed, mankind has been stuck to the idea of two dimensional projectile motion like flies on shit. So long as there is money to be made in selling weapons, and TV stations to keep justifying the legitimacy of the use of these weapons, it is likely that the trend will continue.
It is therefore imperative for anyone interested in reversing this trend to learn about the physics of projectile motion. You need to know the techniques of the enemy (the industrial military complex) before you can fight them. We will see that projectile motion is nothing more than two parallel one-dimensional kinematics problems: UVM in the $x$ direction and UAM in the $y$ direction.
Concepts
The basic concepts of kinematics in two dimensions are:
- $\hat{x},\hat{y}$: a coordinate system.
- $t$: time, measured in seconds.
- $\vec{r}(t)\equiv (x(t),y(t))$: the position (vector) of the object at time $t$.
- $\vec{v}(t) \equiv (v_x(t), v_y(t) ) $: the velocity of the object as a function of time.
- $\vec{a}(t) \equiv (a_x(t), a_y(t) ) $: the acceleration as a function of time.
When solving some problem, where we calculate the motion of an object that starts form an initial point an goes to a final point, we will use the following terminology:
- $t_i=0$: initial time (the beginning of the motion).
- $t_f$: final time (when the motion stops).
- $\vec{v}_{i}=\vec{v}(0)=(v_x(0),v_y(0))=(v_{ix},v_{iy})$: the initial velocity at $t=0$.
- $\vec{r}_i=\vec{r}(0)=(x(0),y(0))=(x_i,y_i)$: the initial position at $t=0$.
- $\vec{r}_f=\vec{r}(t_f)=(x(t_f),y(t_f))=(x_f,y_f)$: the final position at $t=t_f$.
Formulas
Motion in two dimensions
Sometimes you have to describe both the $x$ and the $y$ coordinate of the motion of a particle: \[ \vec{r}(t)=(x(t), y(t)). \] We choose $x$ to be the horizontal component of the projectile motion and $y$ to be its height.
The velocity of the projectile will be \[ \vec{v}(t) = \frac{d}{dt}\left(\vec{r}(t)\right) = \left(\frac{dx(t)}{dt}, \frac{dy(t)}{dt} \right) = (v_x(t),v_y(t)), \] and the initial velocity is: \[ \vec{v}_i = \vec{v}(0) = \|\vec{v}_i\|\angle \theta = (v_x(0), v_y(0)) = (v_{ix}, v_{iy})= (\|\vec{v}_i\|\cos\theta, \|\vec{v}_i\|\sin\theta). \]
The acceleration of the projectile will be: \[ \vec{a}(t) = \frac{d}{dt}\left(\vec{v}(t)\right) = (a_x(t),a_y(t)) = (0,-9.81). \] Note how we have zero acceleration in the $x$ direction (ignoring air friction) so we can use the UVM equations of motion for $x(t)$ and $v_x(t)$. In the $y$ direction we have a uniform downward acceleration due to gravity.
Projectile motion
The equations of motion of a projectile are the following. First in the $x$ direction we have: \[ \begin{align} x(t) & = v_{ix}t + x_i, \nl v_x(t) & =v_{ix}. \end{align} \]
In the $y$ direction, you have the constant pull of gravity downwards which gives us a uniformly accelerated motion (UAM): \[ \begin{align} y(t) & = \frac{1}{2}(-9.81)t^2 + v_{iy}t + y_i, \nl v_y(t) & = -9.81 t + v_{iy}, \nl v_{yf}^2 & = v_{iy}^2 + 2(-9.81)(\Delta y). \end{align} \]
Example
![An object is thrown with 8.96[m/s] at an angle of 51.3 degrees from a height of 1[m].
What will be the maximum height reached and distance travelled by the object? An object is thrown with 8.96[m/s] at an angle of 51.3 degrees from a height of 1[m].
What will be the maximum height reached and distance travelled by the object?](/_media/physics/projecticle-concepts_tikz-0.png?w=400) Let us now consider an example in which we analyze all aspects of the motion of a projectile.
An object is thrown with an initial velocity $8.96$[m/s] at an angle of $51.3^\circ$
with the ground from an initial height of $1$[m].
You are asked to calculate the maximum height $h$ that the object will reach,
and the distance $d$ where the object will hit the ground.
Let us now consider an example in which we analyze all aspects of the motion of a projectile.
An object is thrown with an initial velocity $8.96$[m/s] at an angle of $51.3^\circ$
with the ground from an initial height of $1$[m].
You are asked to calculate the maximum height $h$ that the object will reach,
and the distance $d$ where the object will hit the ground.
Your first step when reading any physics problem should be to extract the information from the problem statement. The initial position is $\vec{r}(0)=(x_i,y_i)=(0,1)$[m]. The initial velocity is $\vec{v}_i=8.96\angle51.3^\circ$[m/s], which is $\vec{v}_i = (8.96\cos51.3^\circ, 8.96\sin51.3^\circ)= (5.6,7)$[m/s] in component form.
You can now plug the values of $\vec{r}_i$ and $\vec{v}_i$ into the equations of motion and find the desired quantities. When the object reaches its maximum height, it will have zero velocity in the $y$ direction: $v_{y}(t_{top})=0$. We can use this fact, and the $v_y(t)$ equation in order to find $t_{top} = 7/9.81= 0.714$[s]. The maximum height is then obtained by evaluating the function $y(t)$ at $t=t_{top}$. We obtain $h = y(t_{top})= 1 + 7(0.714) + \tfrac{1}{2}(-9.81)(0.714)^2 = 3.5$[m].
To find $d$, we must solve the quadratic equation $0=y(t_f)=1 + 7(t_f) + \tfrac{1}{2}(-9.81)(t_f)^2$ to find the time $t_f$ when the object hits the ground. The solution is $t_f=1.55$[s]. We then plug this value into the equation for $x(t)$ to obtain $d= x(t_f)=0 + 5.6(1.55)=8.68$[m]. You can verify that these answers match the trajectory illustrated in the figure.
Explanations
Coordinate system
Before you start to solve any problem, you need to make a diagram of what is going on. On that diagram indicate clearly the coordinate system with respect to which you will measure $x$ and $y$, and $v_x$ and $v_y$. The values you plug into the equations of motion are measured with respect to this coordinate system: a velocity $v_x$ in the opposite direction of the $x$ axis is represented as a negative number.
Uniform velocity motion in the $x$ direction
Ignoring the effects of air friction, there is zero acceleration in the $x$ direction so $a_x=0$. As a consequence, the velocity will be constant. Whatever $x$ velocity you give the projectile when you throw it, it will keep it. Therefore the UVM equations describe its motion in the $x$ direction: \[ \begin{align*} a_x(t) &=0, \nl v_x(t) &= v_{ix}, \nl x(t) &= v_{ix}t + x_{i}. \end{align*} \]
Uniform acceleration motion in the y-direction
We have the pull of gravity in the $y$ direction which is a constant acceleration $a=-9.81$[m/s$^2$], the equations of motion are: \[ \begin{align*} a_y(t) &= - g, \nl v_y(t) &= -gt + v_{iy}, \nl y(t) &= \frac{1}{2}(-g)t^2 + v_{iy}t + y_i, \end{align*} \] where $g=9.81$[m/s$^2$] is the gravitational acceleration on the surface on Earth.
Furthermore we have another useful equation relating the initial and final velocity in the $y$ direction: \[ v_{fy}^2 = v_{iy}^2 + 2a(\Delta y). \] This equation is useful because it does not contain the time.
Examples
Freedom and democracy
An American F-18 is flying above Iraq. It is carrying two bombs. One bomb is called “freedom” and weighs 200[kg], the other “democracy” with mass 500[kg]. If the plane is flying with speed $v_i=300$ [m/s] and drops both bombs from a height of $2000$[m]. How far will the bombs travel? Which city is going to get democracy and which will get freedom?
The equations of motion are: \[ \begin{align*} x(t) &= v_{ix}t + x_{i} = 300 t + 0, \nl y(t) &= \frac{1}{2}(-9.81)t^2 + v_{iy}t + y_{Ai}= -4.9 t^2 + 2000. \end{align*} \] Solving for $t$ in the second equation we get $t=20.20$[s]. We use this value of $t$ in the first equation to find the final $x$ position where the bombs hit the ground $x_f=x(20.20) = 6060$[m]. Both bombs hit the same town, the one which is $6.06$[km] from the launch point. Observe that the masses of the bombs did not play any part in the final equations of motion.
The above scenario is basically what the people in the US state administration are talking about when they say they are bringing freedom and democracy to the Middle East. We have to get those crooked warmongering bastards out of power and quickly. In fact the entire industrial military complex needs to be dismantled because they are the ones who ultimately benefit from the World conflicts. What can we do to stop them you ask? In my opinion, the best way to fight the system is not to work for the system.
Roach throw
You are standing comfortably on a picnic bench in the Parc Mt-Royal and, not far from you, there is a garbage bin. Feeling lazy and relaxed, you decide that you want to throw a particle $r$ into the bin instead of walking over and dropping it in. The particle $r$ (for the French rebut) is a piece of carton rolled upon itself and wrapped in a paper. Imagine a coordinate system centred below your feet. We will denote as $(0,0)$ the point where your right toe touches the ground and the point $(x=0,y=1.4)$[m] is the initial position of the carton $r$ as you are about to flick it with your finger towards the garbage.
Suppose that the garbage bin is 3 metres away from you and that it is 1 metre tall. Can you calculate the initial velocity that the roach needs to have to land in the garbage bin? Assume that you send it flying purely along the $x$-axis, in other words you do not give it any initial $y$-velocity: $v_{iy}=0$. Can you solve for $v_{ix}$ necessary for the roach to fall into the garbage bin?
All that you need to describe the motion of $r$ are the initial
position $\vec{r}(0)=(x(0), y(0))$ and the initial
velocity $\vec{v}_i = \vec{v}(0) = (v_x(0), v_y(0))$,
which you can then plug into the equations of motion:
\[
\begin{align*}
x(t) &= v_{ix}t + x_i, \nl
y(t) &= y_i + v_{iy}t + \frac{1}{2}a_y t^2.
\end{align*}
\]
Most physics word problems will follow this pattern.
The problem statement gives you some information
about the initial conditions and the desired final conditions
and then ask you to solve for the unknown,
i.e., the one variable which they didn't give you.
Can you carry out the necessary calculations in this case? I don't mean to stress you out, but sitting next to you is your 110kg pure-muscle Chilean friend who has two kids and really gets pissed off at people who throw garbage around in the park. You don't want to piss him off so you better get that initial velocity right!
OK, from now on we can switch into high gear because we have everything setup nicely for us. We know that the general equations of motion for UVM in $x$ and UAM in $y$ are: \[ \begin{align*} x(t) &= v_{ix}t + x_i, \nl y(t) &= y_i + v_{iy}t + \frac{1}{2}a_y t^2, \end{align*} \] and more specifically we know that the $y$ acceleration is due to gravity so we have: \[ \begin{align*} x(t) &= v_{ix}t + x_i, \nl y(t) &= y_i + v_{iy}t + \frac{1}{2}(-9.81)t^2. \end{align*} \]
We also know that the position at $t=0$ is $(x_i, y_i) = (0,1.4)$ and that at some $t_f>0$ we will be flying through the bin at $(x(t_f), y(t_f)) = (3,1)$.
Thus we have: \[ \begin{align*} x(t_f) = 3 &= v_{ix}t_f + 0, \nl y(t_f) = 1 &= 1.4 + v_{iy}t_f + \frac{1}{2}(-9.81)t_f^2. \end{align*} \]
Furthermore, since the problem specified it, we can assume that
the initial velocity of $r$ was purely horizontal ($v_{iy}=0$).
Thus, the equations we have to solve are:
\[
\begin{align*}
\qquad \ \ \: 3 &= v_{ix}t_f, \nl
\qquad \ \ \: 1 &= 1.4 -4.9 t^2_f,
\end{align*}
\]
where $v_{ix}$ and $t_f$ are the two unknowns.
From here on, it should be clear where the story is going. First we solve for $t_f$ in the second equation: \[ t_f = \sqrt{ \frac{(1-1.4)}{-4.9} } = \sqrt{ \frac{-0.4}{-4.9} } = \sqrt{ 4/49} = 2/7 \approx 0.28571.. , \qquad \text{[s]} \] and plug that into the first equation to solve for $v_{ix}$ as follows: \[ v_{ix} = \frac{3}{t_f} = \frac{3\cdot 7}{2} = \frac{21}{2} = 10.5 \qquad \text{ [m/s]. } \]
You flick $r$ with you finger at an initial velocity of exactly $\vec{v}_i =(10.5,0)$[m/s] and the roach flies right into the garbage bin. Success!
Interception
With all those people lunging explosive projectiles at each other, a need develops for interception systems which can throw a counter-projectile at the incoming projectile and knock it out of the air.
Let us study how we can intercept an incoming ball (A) launched from $\vec{r}_{Ai}=(0,3)$ with initial velocity $\vec{v}_{Ai}=(8\cos(40), 8\sin(40))$. As interception device, you have at your disposal a ball launcher placed at $\vec{r}_{Bi}=(10,0)$ with a fixed firing angle of $50^\circ$ placed so that it faces the incoming ball. The ball launcher has a variable launch speed $w$[m/s], which you can choose. You want to fire an intercepting ball, which will have initial velocity $\vec{v}_{Bi}=(-w\cos(50), w\sin(50))$ so as to intercept the ball (A) in mid-air. What is the required initial velocity $w$ for the balls to hit each other? At which time $t$ will the collision take place?
As far as kinematics is concerned, this is a standard projectile motion problem times two. You have ball (A) which has equations of motion: \[ \begin{align*} x_A(t) &= v_{Aix}t + x_{Ai} = 8\cos(40) t + 0, \nl y_A(t) &= \frac{1}{2}(-9.81)t^2 + v_{Aiy}t + y_{Ai}= -4.9 t^2 + 8\sin(40) t + 3, \end{align*} \] and ball (B) which has equations of motion: \[ \begin{align*} x_B(t) &= v_{Bix}t + x_{Bi} = - w \cos(50) t + 10, \nl y_B(t) &= \frac{1}{2}(-9.81)t^2 + v_{Biy}t + y_{Bi}= -4.9 t^2 + w\sin(50) t + 0. \end{align*} \]
The fact that we want the balls to collide, means that at some point they will have the same coordinates $\vec{r}_A = \vec{r}_B$, which is another way of saying \[ (x_A(t), y_A(t)) = (x_B(t), y_B(t)). \] The $x$-coordinates have to match, and the $y$-coordinates have to match, so this gives us two equations: \[ \begin{align} 8\cos(40) t + 0 &= - w \cos(50) t + 10, \nl -4.9 t^2 + 8\sin(40) t + 3 &= -4.9 t^2 + w\sin(50) t + 0. \end{align} \]
We can cancel the $-4.9 t^2$ on both sides of the bottom equation to get: \[ \begin{align} 8\cos(40) t &= - w \cos(50) t + 10, \nl 8\sin(40) t + 3 &= w\sin(50) t. \end{align} \]
This is a set of two equations with two unknowns, so we can solve it. It is not going to be easy to do this, because we can't isolate either of $t$ or $w$ in a clean way using the standard substitution techniques. There is a trick though: we can divide the two equations! If $A=B$ and $C=D\neq 0$ then $A/C = B/D$ so this is what we will use. In preparation for this step, let me rearrange the equations a bit to have all the $w$-containing terms alone on the right side: \[ \begin{align} 10 - 8\cos(40) t &= w \cos(50) t , \nl 8\sin(40) t + 3 &= w \sin(50) t. \end{align} \]
We will now divide the bottom equation by the top equation to obtain: \[ \frac{ 8\sin(40) t + 3 }{10 - 8\cos(40) t} = \frac{ w \sin(50) t }{ w \cos(50) t} = \tan(50). \]
Rearranging the expression we get \[ 8\sin(40) t + 3 = \tan(50)( 10 - 8\cos(40) t ). \] We now collect all the $t$ terms to one side to obtain: \[ [8\sin(40) + 8\cos(40)\tan(50)] t = 10\tan(50) - 3, \] and finally \[ t = \frac{10\tan(50) - 3}{ 8\sin(40) + 8\cos(40)\tan(50) } = 0.7165 \text{[s]}. \]
We can now plug into any of the above equations to find the value of $w$. For example plugging the value of $t=0.7165$ into \[ 10 - 8\cos(40) t = w \cos(50) t, \] we will get \[ 10 - 8\cos(40)(0.7165) = w \cos(50)(0.7165), \] and so $w = \frac{10 - 8\cos(40)(0.7165)}{ \cos(50)(0.7165)} = 12.1788$ [m/s].
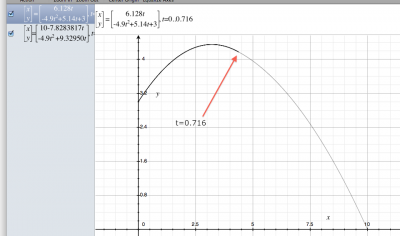
OK. Now let's check our answer. If we use the initial velocity $12.1788$ and substitute that into the equations of motion for ball (B), and plot the two trajectories on the computer:
They do meet indeed and at the specified time $t=0.7165$[s].
Discussion
I want to point out that there is no new physics necessary to understand the motion of projectiles. Projectile motion is a two-dimensional kinematics problem which can be broken down into two parts: the $x$ direction (described by the UVM equations) and the $y$ direction (described by the UAM equations).
Links
[ Eisenhower on the danger posed by the industrial military complex. ]
Quote: “Only an alert and knowledgeable citizenry can compel the proper
meshing of the huge industrial and military machinery of defence with
our peaceful methods and goals.”
http://www.youtube.com/watch?v=8y06NSBBRtY
}
Forces
Like a shepherd who brings back stray sheep, we need to rescue the word force and give it precise meaning. In physics force means something very specific. Not “the force” from Star Wars, not the “force of public opinion”, and not the force in the battle of good versus evil.
Force in physics has a precise meaning as an amount of push or pull exerted on an object. Forces are vector quantities measured in Newtons [N]. In this section we will explore all the different kinds of forces.
Concepts
- $\vec{F}$: a force. This is something the object “feels” as a pull or a push. Force is a vector, so you must always keep in mind the direction in which the force $\vec{F}$ acts.
- $k,G,m,\mu_s,\mu_k,\ldots$: parameters on which the force $F$ may depend. Ex: the heavier an object is (large $m$ parameter), the larger its gravitational pull will be: $\vec{W}=-9.81m\hat{\jmath}$, where $\hat{\jmath}$ points towards the sky.
Kinds of forces
We next list all the forces which you are supposed to know about for a standard physics class and define the relevant parameters for each kind of force. You need to practice exercises using each of these forces, until you start to feel how they act.
Gravitation
The force of gravity exists between any two massive objects. The magnitude of the gravitational force between two objects of mass $M$[kg] and $m$[kg] separated by a distance $r$[m] is given by the formula \[ F_g=\frac{GMm}{r^2}, \] where $G=6.67 \times 10^{-11}$[$\frac{\text{Nm}^2}{\text{kg}^2}$] is the gravitational constant. This is the famous one-over-arr-squared law that describes the gravitational pull between two objects. This was Newton's big discovery.
On the surface of the earth, which has mass $M=5.972\times 10^{24}$[kg] and radius $r=6.367\times10^6$[m], the force of gravity on an object of mass $m$ is given by \[ F_g=\frac{GMm}{r^2} = \underbrace{\frac{GM}{r^2}}_{g}m = 9.81 m = W. \] We call this force the weight of the object and to be precise we should write $\vec{W}=-mg\hat{\jmath}$ to indicate that the force acts downwards—in the negative $y$ direction. Verify using your calculator that $\frac{GM}{r^2}=9.81\equiv g$.
Force of a spring
A spring is a piece of metal twisted into a coil that has a certain natural length. The spring will resist any attempts to stretch it or compress it. The force exerted by a spring is given by \[ \vec{F}_s=-k\vec{x}, \] where $x$ is the amount by which the spring is displaced from its natural length and the constant $k$[N/m] is a measure of the strength of the spring. Note the negative sign: if you try to stretch the spring (positive $x$) then the force of a spring will pull against you (in the negative $x$ direction), if you try to compress the spring (negative $x$) it will push back against you (in the positive $x$ direction).
Normal force
The normal force is the force between two surfaces in contact. The word normal means “perpendicular to the surface of” in this context. The reason why my coffee mug does not fall to the floor right now is that the table exerts a normal force $\vec{N}$ on it keeping in place.
Force of friction
In addition to the normal force between surfaces, there is also the force of friction $\vec{F}_f$ which acts to prevent or slow down any sliding motion between the surfaces. There are two kinds of force of friction and both kinds of are proportional to the amount of normal force between the surfaces: \[ \max \{ \vec{F}_{fs} \}=\mu_s\|\vec{N}\| \ \ \text{(static)}, \qquad \vec{F}_{fk}=\mu_k\|\vec{N}\| \ \ \text{(kinetic)}, \] where $\mu_s$ and $\mu_k$ are the static and dynamic friction coefficients. Note that it makes intuitive sense that the force of friction should be proportional to the magnitude of the normal force $\|\vec{N}\|$: the harder the surfaces push against each other the more difficult it should be to make them slide. The above equations make this intuition precise.
The static force of friction acts on objects that are not moving. It describes the maximum amount of friction that can exist between two objects. If a horizontal force greater than $F_{fs} = \mu_s N$ is applied to the object, then it will start to slip. The kinetic force of friction acts when two objects are sliding relative to each other. It always acts in the direction opposite to the motion.
Tension
A force can also be exerted on an object remotely by attaching a rope to the object. The force exerted on the object will be equal to the tension in the rope $\vec{T}$. Note that tension always pulls away from an object: you can't push a dog on a leash.
Discussion
Viewing the interactions between objects in terms of the forces that act between them is a very powerful way of thinking. In the next section, we will learn how to draw force diagrams which take into account all the forces that act on the object.
Force diagrams
Welcome to Force-Accounting 101. In this section we will learn how to identify all the forces acting on an object and use Newton's 2nd law $\sum \vec{F}=\vec{F}_{net} = m\vec{a}$ to predict the resulting acceleration.
Concepts
Newton's second law describes a relationship between these three quantities:
- $m$: the mass of an object.
- $\vec{F}_{net}$: the net force on the object.
- $\vec{a}$: the acceleration of the object.
Forces and accelerations are vectors. To work with vectors, we work with their components:
- $F_x$: the component of $\vec{F}$ in the $x$ direction.
- $F_y$: the component of $\vec{F}$ in the $y$ direction.
Vectors are meaningless unless it is clear with respect to which coordinate system they are expressed.
- $x$ axis: Usually the $x$ axis is horizontal and to the right, however, for problems with inclines,
it will be more convenient to use an inclined $x$ axis that is parallel to the slope.
- $y$ axis: The $y$ axis is always perpendicular to the $x$ axis.
- $\hat{\imath},\hat{\jmath}$: Unit vectors in the $x$ and $y$ directions. Any vector can be written as $\vec{v}=v_x\hat{\imath}+v_y\hat{\jmath}$ or as $\vec{v}=(v_x,v_y)$.
Provided we have a coordinate system, we can write any force vector in three equivalent ways: \[ \vec{F} \equiv F_x\hat{\imath} + F_y\hat{\jmath} \equiv (F_x,F_y) \equiv \|\vec{F}\|\angle \theta. \]
What types of forces are there in force diagrams?
- $\vec{W}\equiv\vec{F}_{gravity}=m\vec{g}$: The weight. This is the force on a object due to its gravity. The gravitational pull $\vec{g}$ always points downwards – towards the centre of the earth. $g=9.81$[N/kg].
- $\vec{T}$: Tension in a rope. Tension is always pulling away from the object.
- $\vec{N}$: Normal force – the force between two surfaces.
- $\vec{F}_{fs}=\mu_s\|\vec{N}\|$: Static force of friction.
- $\vec{F}_{fk}=\mu_k\|\vec{N}\|$: Kinetic force of friction.
- $\vec{F}_{s}=-kx$: The force (pull or push) of a spring that is displaced (stretched or compressed) by $x$ metres.
Formulas
Newton's 2nd law
The sum of the forces acting on an object, divided by the mass, gives you the acceleration of the object: \[ \sum \vec{F} \equiv \vec{F}_{net}= m\vec{a}. \]
Vector components
If a vector $\vec{v}$ makes an angle $\theta$ with the $x$ axis then: \[ v_x = \|\vec{v}\|\cos\theta, \qquad \text{and} \qquad v_y = \|\vec{v}\|\sin\theta. \] The vector $v_x\hat{\imath}$ corresponds to the part of $\vec{v}$ that points in the $x$ direction.
In what follows, you will be asked a countless number of times to \[ \text{Find the component of } \vec{F} \text{ in the ? direction. } \] Which is another way of asking you to find the number $v_?$.
The answer is usually equal to the length $\|\vec{F}\|$ multiplied by either $\cos$ or $\sin$ and sometimes $-1$ all depending on way the coordinate system is chosen. So don't guess. Look at the coordinate system. If the vector points in the direction where $x$ increases, then $v_x$ should be a positive number. If $\vec{v}$ points in the opposite direction, then $v_x$ should be negative.
To add forces $\vec{F}_1$ and $\vec{F}_2$ you have to add their components: \[ \vec{F}_1 + \vec{F}_2 = (F_{1x},F_{1y}) + (F_{1x},F_{2y}) = (F_{1x}+F_{2x},F_{1y}+F_{2y}) = \vec{F}_{net}. \] Instead of dealing with vectors in the bracket notation as above, when solving force diagrams it is easier to simply write the $x$ equation on one line, and the $y$ equation on a separate line below it: \[ F_{netx} = F_{1x}+F_{2x}, \] \[ F_{nety} = F_{1y}+F_{2y}. \] It is a good idea to always write those two equations together as a block – so it remains clear that you are talking about the same problem, but the first row represents the $x$-dimension and the second row represents the $y$-dimension.
Force check
It is important to account for all the forces acting on an object. Any object with mass on the surface of the earth will feel a downwards gravitational pull of magnitude $F_{g}=W=m\vec{g}$. Then you have to think about which of the other forces might be present: $\vec{T}$, $\vec{N}$, $\vec{F}_{f}$, $\vec{F}_{s}$. Anytime you see a rope tugging on the object, you know there must be some tension $\vec{T}$, which is a force vector pulling on the block. Anytime you have an object sitting on a surface, the surface will push back with a normal force $\vec{N}$. If the object is sliding on the surface there will be a force of friction acting against the direction of the motion: \[ F_{fk}=\mu_k\|\vec{N}\|. \] If the object is not moving, then you have to use $\mu_s$ in the friction force equation, to get the maximum static friction force that the contact between the object and the ground can support before the object starts to slip: \[ \max\{ F_{fs} \}=\mu_s\|\vec{N}\|. \] If you see a spring that is either stretched or compressed by the object, then you must account for the spring force. The force of a spring is restorative: it always acts against the deformation you are making to the spring. If you stretch it by $x$[cm], then it will try to pull itself back to its normal length with a force of: \[ \vec{F}_s = -kx \hat{\imath}. \] The constant of proportionality $k$ is called the spring constant and is measured in [N/m].
Recipe for solving force diagrams
Below we list the steps of the general procedure to follow when solving problems in dynamics.
- Draw a force diagram focussed on the object and indicate all the forces acting on it.
- Choose a coordinate system, and indicate clearly in the diagram what you will call the positive $x$ direction, and what you will call the positive $y$ direction. All quantities in the subsequent equations will be expressed with respect to this coordinate system.
- Write down the following “template”:
\[ \sum F_x = \qquad \qquad \qquad = ma_x, \] \[ \sum F_y = \qquad \qquad \qquad = ma_y. \]
- Fill in the template by calculating the $x$ and $y$ components
of each force acting on the object:
$\vec{W}$, $\vec{N}$, $\vec{T}$, $\vec{F}_{fs}$, $\vec{F}_{fk}$,
$\vec{F}_{s}$ as applicable.
- Solve the equations for the unknown quantities.
I highly recommend that you perform some consistency checks after Step 4. You should check the signs: if the force in the diagram is acting in the $x$ direction, then its component must be positive. If the force is acting in the direction opposite to the $x$ axis, then its component should be negative. You should also check that whenever $F_x \propto \cos\theta$, then $F_y \propto \sin\theta$. If instead we use the angle $\phi$ defined with respect to the $y$ axis, we would have $F_x \propto \sin\phi$, and $F_y \propto \cos\phi$.
We will now illustrate how to use this recipe through a series of examples.
Examples
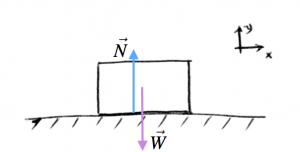
Block on a table
You place a block of mass $m$ on the table. If it has mass $m$ then it feels its weight $\vec{W}$ pulling down on it, but the table is not letting it drop to the floor. The table pushes back on the block with a normal force $\vec{N}$.
Steps 1,2: We draw the force diagram and choose a coordinate system:
Step 3: Next, we write down the empty equations template: \[ \begin{align*} \sum F_x &= \qquad \qquad = ma_x, \nl \sum F_y &= \qquad \qquad = ma_y. \end{align*} \]
Step 4: There is nothing much going on in the $x$ direction: no forces acting in the $x$ direction and the block is not moving so $a_x=0$. In the $y$ direction we have the force of gravity and the normal force exerted by the table: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \] We set $a_y=0$, because we see that the block is just sitting there on the table without moving. The technical term for situations where $a_x=0, a_y=0$ is called static equilibrium. Force diagrams with static equilibrium are easy to solve, because the entire right-hand side is equal to zero, which means that the forces on the object must be counter-balancing each other.
Step 5: Suppose the teacher was asking you “What is the magnitude of the normal force?”. You can easily answer this by looking at the second equation: “$N=mg$ bro!”
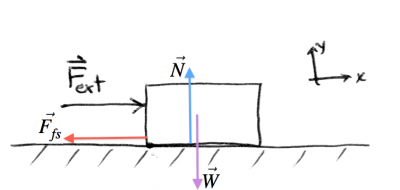
Moving the fridge
You are trying to push your fridge across the kitchen floor. Because it weights quite a lot, it is “gripping” the floor quite a bit. If the static coefficient of friction between the metal “feet” of your fridge and the tiles of the floor is $\mu_s$, how much force $\vec{F}_{ext}$ would it take to get the fridge to start moving?
\[ \begin{align*} \sum F_x &= F_{ext} - F_{fs} = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
If you push with force $F_{ext}=30$[N], the fridge will push back (via its connection to the floor) with a force $F_{fs}=30$[N]. If you push harder, the fridge will push back harder and it will still not move. Only when you reach the slipping threshold will it move. This means you have to push with force equal to the maximum static friction force $F_{fs}=\mu_s N$, so we have: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_s N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
To solve for $F_{ext}$ you first isolate $N=mg$ in the bottom line, and then substitute the value of $N$ in the top line to get $F_{ext} = \mu_s m g$.
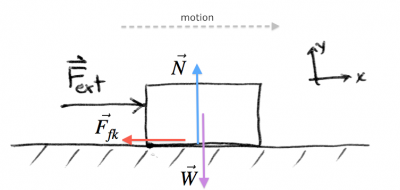
Friction slowing you down
OK, so you have the fridge moving now and you are moving at a steady pace across the room:
Your equation of motion is going to be: \[ \begin{align*} \sum F_x &= F_{ext} - \vec{F}_{fk} = ma_x, \nl \sum F_y &= N - mg = 0. \end{align*} \]
In particular if you want to keep a steady speed ($v=const$) as you move across the room, you will push with such a force just to balance the friction force and keep $a_x=0$.
To find the value of $F_{ext}$ to keep a constant speed we solve: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_k N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
We get a similar expression as above, but with $\mu_k$ instead of $\mu_s$: $F_{ext} = \mu_k m g$. Generally, $\mu_k < \mu_s$ so it takes less force to keep the fridge moving than it took to get it to start moving.
Let us now take a different slant on this whole friction thing.
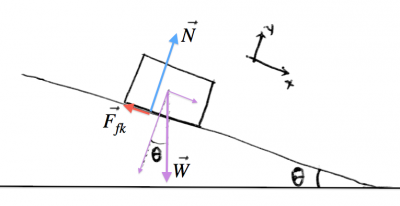
Incline
At this point, my dear readers, we are getting into the main kind of question that will be, without a doubt, asked in your homework or at the final exam. A block sliding down an incline. What is its acceleration?
Step 1: We draw a diagram which includes the weight $\vec{W}$, the normal force $\vec{N}$ and the friction force $\vec{F}_{fk}$.
Step 2: We pick the coordinate system to be tilted along the incline. This is important because this way the motion is purely in the $x$ direction, while the $y$ direction will be static.
Step 3,4: Let's copy the empty template, and fill in the equations: \[ \begin{align*} \sum F_x &= \|\vec{W}\|\sin\theta - F_{fk} = ma_x, \nl \sum F_y &= N - \|\vec{W}\|\cos\theta \ \ = 0, \end{align*} \] or substituting the values that we know: \[ \begin{align*} \sum F_x &= mg\sin\theta - \mu_kN = ma_x, \nl \sum F_y &= N - mg\cos\theta \ \ \ = 0. \end{align*} \]
Step 5: From the $y$ equation, we obtain $N=mg\cos\theta$ and substituting this into the $x$ equation we get: \[ a_x = \frac{1}{m}\left( mg\sin\theta - \mu_k mg\cos\theta \right) = g\sin\theta - \mu_k g\cos\theta. \]
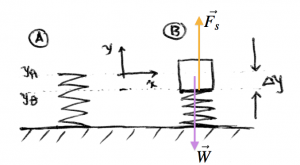
Bathroom scale
You have a spring with spring constant $k$ on which you put a block of mass $m$. By what length $\Delta y$ will the spring be compressed?
Step 1,2: We draw a before and after picture, with the $y$ axis placed at the natural length of the spring.
Step 3,4: Filling in the template we get: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= F_s - mg = 0. \end{align*} \]
Step 5: We know that the force exerted by a spring is proportional to its displacement according to \[ F_s = -k y_B, \] so we can find $y_B = -\frac{mg}{k}$. The length of compression is therefore: \[ |\Delta y| = \frac{mg}{k}. \]
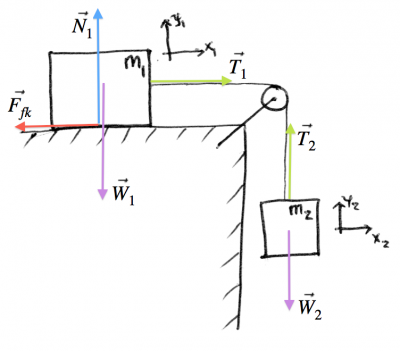
Two blocks
Now for a more involved example with two blocks. One block is sitting on the surface, and another one is falling straight down. The two are connected by a stiff rope. What is the acceleration of the system as a whole?
Steps 1,2: We have two objects, so we have to draw two force diagrams.
Step 3: We also have two sets of equations. One set of equations for the left block, and one for the right block: \[ \begin{align*} & \sum F_{1x} = \qquad\qquad = m_1a_{x_1} & \qquad & \sum F_{2x} = \qquad\quad = m_2a_{x_2} \nl & \sum F_{1y} = \qquad\qquad = m_1a_{y_1} & \qquad & \sum F_{2y} = \qquad\quad = m_2a_{y_2} \end{align*} \]
Steps 4: We fill them in with all the forces drawn in the diagram: \[ \begin{align*} & \sum F_{1x} = -F_{fk} + T_1 = m_1a_{x_1} & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - W_1 = 0 & \qquad & \sum F_{2y} = -W_2 + T_2 = m_2a_{y_2} \end{align*} \]
Step 5: What are the connections between the two blocks? Since it is the same rope that connects the two blocks, this means that the tension in the rope is the same on both ends so $T_1=T_2=T$. Also since the rope is of fixed length we have that the $x_1$ and $y_2$ coordinates are related by a constant (though they point in different directions), so it must be that $a_{x_1}= -a_{y_2} = a$.
Rewriting in terms of the new common variables $T$ and $a$ we have: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - m_1g = 0 & \qquad & \sum F_{2y} = -m_2g + T = - m_2a \end{align*} \]
We isolate $N_1$ on the bottom left, and isolate $T$ on the bottom right: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & N_1 = m_1g & \qquad & T = - m_2a + m_2g \end{align*} \]
Now substitute the values into the top left equation to get \[ \sum F_{1x} = -\mu_k(m_1g) + (- m_2a + m_2g) = m_1 a, \] or moving all the $a$ terms to one side we have \[ -\mu_km_1g + m_2g = m_1 a + m_2 a = (m_1 + m_2) a, \] which makes sense since the “two blocks attached with a rope” is in some sense an object of collective mass $(m_1 + m_2)$ with two external forces on it. From this point of view, the tension $T$ is an internal force of the object and doesn't appear in the external force equation.
The acceleration of the whole two-block system going to be: \[ a = \frac{m_2g - \mu_km_1g}{m_1+m_2}. \]
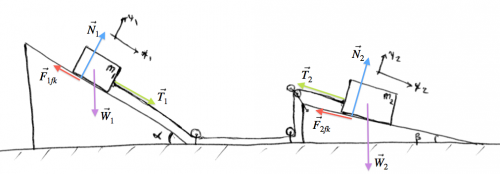
Two inclines
OK, let's just go crazy now! Let's have two inclines, two blocks, a rope, and friction everywhere. We want to find the acceleration as usual.
Steps 1,2: We draw a force diagram with two different coordinate systems each adapted for the angle of the incline:
Steps 3,4: Fill in all force components, and set $a_{y_1}=0,a_{y_2}=0$: \[ \begin{align*} & \sum F_{1x} = W_1\sin\alpha - F_{1fk} + T_1 = m_1a_{x_1}, \nl & \sum F_{1y} = -W_1\cos\alpha + N_1 \quad \ \ \ = 0, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = W_2\sin\beta - F_{2fk} - T_2 = m_2a_{x_2}, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2y} = -W_2\cos\beta + N_2 \quad \ \ \ =0. \end{align*} \]
Step 5: The links between the two worlds are two: the tension in the rope is the same $T=T_1=T_2$ and also the acceleration since the blocks are moving together $a=a_{x_1}=a_{x_2}$. Rewriting and expanding we have: \[ \begin{align*} & \sum F_{1x} = m_1g\sin\alpha - \mu_k N_1 + T = m_1a, \nl & N_1 = m_1g\cos\alpha, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k N_2 - T = m_2a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad N_2 = m_2g\cos\beta. \end{align*} \]
Let's substitute the values of $N_1$ and $N_2$ into the $x$ equations: \[ \begin{align} & \sum F_{1x} = m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k m_2g\cos\beta - T = m_2a. \end{align} \]
There are many ways to solve for the two unknowns in this pair of equations. Either (A) we isolate $T$ in one of the equations and substitute the value of $T$ into the second or (B) we isolate $a$ in both equations and set them equal to each other.
We will use approach (A) and isolate $T$ in the bottom equation to get: \[ \begin{align} & m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a = T. \end{align} \] and finally substitute the expression for $T$ into the top equation to obtain \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + ( m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a) = m_1a, \] which can be rewritten as \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + m_2g\sin\beta - \mu_k m_2g\cos\beta = (m_1 + m_2)a. \] Since we know the values of $m_1$, $m_2$, $\mu_k$, $\alpha$ and $\beta$, we can calculate all the quantities on the left-hand side and solve for $a$.
Other types of problems
All the examples shown asked you to find the acceleration, but sometimes you might be told the acceleration and asked to solve for some other unknown in the equations. Regardless of what you have to solve for, you should always start with the diagram and the sum-of-the-forces template. Once you have these equations in front of you, you will be able to reason about the problem more easily.
Experiment
Suspend an object of known mass (say a 100g chocolate bar) on the spring taken out from a retractable pen. Use a ruler to measure by how much the spring stretches in the process. What is the spring constant $k$?
Discussion
In previous sections we discussed the kinematics problem of finding the position of an object $x(t)$ given the knowledge of its acceleration function $a(t)$ and the initial conditions $x_i$ and $v_i$. In this section we studied the dynamics problem, which involved drawing force diagrams and calculating the net force on the object. Understanding these topics means that you fully understand Newton's equation $F=ma$ which is perhaps the most important equation in this book.
We can summarize the entire procedure for predicting the position of an object $x(t)$ from first principles in the following equation: \[ \frac{1}{m} \underbrace{ \left( \sum \vec{F} = \vec{F}_{net} \right) }_{\text{dynamics}} = \underbrace{ a(t) \ \overset{v_i+ \int\!dt }{\longrightarrow} \ v(t) \ \overset{x_i+ \int\!dt }{\longrightarrow} \ x(t) }_{\text{kinematics}}. \] The left-hand side calculates the net force, which is the cause of acceleration. The right-hand side indicates how we can calculate the equation of motion $x(t)$ from the knowledge of the acceleration and the initial conditions. This means that if you know the forces acting on any object (rocks, projectiles, cars, stars, planets, etc.) then we can predict its motion, which is kind of cool.
Momentum
During a collision between two objects there will be a sudden spike in the contact force between them, which can be difficult to measure and quantify. It is therefore not possible to use Newton's law $F=ma$ to predict the accelerations that occur during collisions. In order to predict the motion of the objects after the collision we must use a momentum calculation. The law of conservation of momentum states that the total amount of momentum before and after the collision is the same. Thus, if we know the momenta of the objects before the collision, it will be possible to calculate their momenta after the collision and from this figure out their subsequent motion.
To illustrate why the notion of momentum is important, consider the following situation. Say you have a 1[g] piece of paper and a 1000[kg] car moving at the same speed 100[km/h]. Which of the two objects would you rather get hit by? Momentum, denoted $\vec{p}$, is the precise physical concept which measures the “amount of moving stuff”. An object of mass $m$ moving with velocity $\vec{v}$ has momentum $\vec{p}\equiv m\vec{v}$. Momentum plays a key role in collisions, so your gut feeling about the piece of paper and the car is correct. The car weights $1000\times1000=10^{6}$ times more than the piece of paper, so it has $10^6$ times more momentum when moving at the same speed. A collision with the car will “hurt” a million times more than the collision with the piece of paper even though they were moving at the same speed.
In this section we will learn how to use the law of conservation of momentum to predict the outcomes of collisions.
Concepts
- $m$: the mass of the moving object.
- $\vec{v}$: the velocity of the moving object.
- $\vec{p}=m\vec{v}$: the momentum of the moving object.
- $\sum \vec{p}_{in}$: the sum of the momenta of particles before a collision.
- $\sum \vec{p}_{out}$: the sum of the momenta after the collision.
Definition
The momentum of a moving object is equal to the velocity of the moving object multiplied by the object's mass: \[ \vec{p} = m\vec{v} \qquad [\text{kg}\:\text{m}/\text{s}]. \] If the velocity of the object is $\vec{v}=20\hat{\imath}=(20,0)$[m/s] and it has a mass of 100[kg] then its momentum is $\vec{p}=2000\hat{\imath}=(2000,0)$[kg$\:$m/s].
Momentum is a vector quantity, so we will often have to convert momentuma from the length-and-direction form to the components form: \[ \vec{p}= \|\vec{p}\| \angle \theta = (\|\vec{p}\|\cos\theta, \|\vec{p}\|\sin\theta) = (p_x, p_y). \] The component form makes it easy to add and subtract vectors: $\vec{p}_1 + \vec{p}_2 = (p_{1x}+p_{2x},p_{1y}+p_{2y})$. To express the final answer, we will have to convert from the component form back to the length-and-direction form using: \[ \|\vec{p}\| = \sqrt{ p_x^2 + p_y^2 }, \qquad \theta = \tan^{-1}\!\left( \frac{ p_{y} }{ p_{x} } \right). \]
Conservation of momentum
Newton's first law states that in the absence of acceleration ($\vec{a}=0$), an object will maintain a constant velocity. This is kind of obvious if you know Calculus, since $\vec{a}$ is the derivative of $\vec{v}$. For example, if an object is stationary and there are no forces on it to cause it to accelerate, then it will remain stationary. If an object is moving with velocity $\vec{v}$ and there is no acceleration (or deceleration), then it will keep moving with velocity $\vec{v}$ forever. In the absence of acceleration, objects will conserve their velocity: \[ \vec{v}_{in}= \vec{v}_{out}. \] This is equivalent to saying that objects conserve their momentum (just multiply the velocity by the constant mass of the object).
More generally, if you have a situation involving multiple moving objects, you can say that the “overall momentum”, i.e., the sum of the momenta of all the interacting particles stays constant. This reasoning is particularly useful when analyzing collisions since it allows us to connect the sum of the momenta before the collision and after the collision: \[ \sum \vec{p}_{in} = \sum \vec{p}_{out}. \] Whatever momentum comes into a collision must come out. This equation is known as the law of conservation of momentum.
This conservation law is one of the furthest reaching laws of physics you will learn in Mechanics. We learned about the conservation of momentum in a simple context of two colliding particles, but the law applies much more generally: for multiple particles, for fluids, for fields, and even for collisions involving atomic particles described by quantum mechanics. The quantity of motion (momentum) cannot be created or destroyed, it can only be exchanged between systems.
Examples
Example 1
You throw a piece of rolled up carton of mass $0.4$[g] from your balcony on a rainy day. You throw it horizontally with a speed of 10[m/s]. Shortly after it leaves your hand it collides with a rain drop of weight $2$[g] falling straight down at a speed of $30$[m/s]. What will be resulting velocity if the two objects stick together after the collision?
The conservation of momentum equation says that: \[ \vec{p}_{in,1} + \vec{p}_{in,2} = \vec{p}_{out}. \] Plugging in the values we get \[ 0.4\times (10,0) \ \ + \ \ 2\times (0,-30) \ \ = \ \ 2.4 \times \vec{v}_{out}, \] or solving for $\vec{v}_{out}$ we find: \[ \vec{v}_{out} = \ \frac{ 0.4(10,0) - 2 (0,30)} {2.4} = (1.666, - 25.0) = 1.666\hat{\imath} - 25.0\hat{\jmath}. \]
Example 2: Hipsters on bikes
Two hipsters on single-speed bicycles are headed towards the same intersection. Say they are both speeding down Parc street at 50[km/h] and the first hipster is crossing the street at a diagonal of 30 degrees when they collide. I mean you saw this coming right? Well the second hipster didn't, because he was busy turning the pedals as fast as he can.
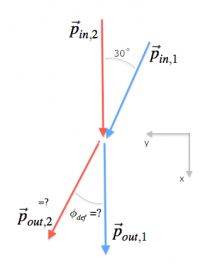 Let us assume that the combined weight of the straight-going hipster and his bike is 100[kg],
whereas the street-crossing-at-30-degrees hipster has a lighter, more expensive bicycle frame.
We put his weight at 90[kg].
Let us assume that the combined weight of the straight-going hipster and his bike is 100[kg],
whereas the street-crossing-at-30-degrees hipster has a lighter, more expensive bicycle frame.
We put his weight at 90[kg].
(I am going to continue with the story, but I want to point out that we have been given, the following information so far: \[ \begin{align*} \vec{p}_{in,1} &= 90\times50 \angle 30=90(50\cos30,50\sin30), \nl \vec{p}_{in,2} &= 100\times50 \angle 0=(5000,0), \end{align*} \] where the $x$ coordinate points down Park street, and the $y$ coordinate is perpendicular to the street.)
Surprisingly, nobody gets hurt in this collision. They bump shoulder-to-shoulder and the one that was trying to cross the street gets redirected straight down the street, while the one going straight down gets deflected to the side and right onto the bike path. I know what you are thinking: couldn't they get hurt at least a little bit? OK, let's say that the whiplash from their shoulder-to-shoulder collision sends their heads flying towards each other and their glasses get smashed. There you have it.
Suppose the velocity of the first hipster after the collision is 60 [km/h], what is the velocity and the deflected direction of the second hipster? (I have just told you that the outgoing momentum of the first hipster is $\vec{p}_{out,1}=(90\times60,0)$, and asked you to find $\vec{p}_{out,2}$.)
We can solve this problem using the conservation of momentum formula, which tells us that: \[ \vec{p}_{in,1} + \vec{p}_{in,2} = \vec{p}_{out,1} + \vec{p}_{out,2}. \] We know three of the above quantities so we can solve for the one (vector) unknown by isolating it on one side of the equation: \[ \vec{p}_{out,2} = \vec{p}_{in,1} + \vec{p}_{in,2} - \vec{p}_{out,1}, \] \[ \vec{p}_{out,2} = 90(50\cos30,50\sin30)\ +\ (5000,0)\ - \ (90\times60,0). \] The $x$ component of the momentum $\vec{p}_{out,2}$ is: \[ p_{out,2,x} = 90\times50\cos30 + 5000 - 90\times 60 = 3497.11, \] and the $y$ component is $p_{out,2,y} = 90\times 50\sin30 = 2250$.
The magnitude of the momentum of hipster 2 is given by: \[ \|\vec{p}_{out,2}\| = \sqrt{ p_{out,2,x}^2 + p_{out,2,y}^2 } = 4158.39, \quad \textrm{[kgkm/h]}. \] Note the units we use for the momentum is not the standard choice [kgm/s]. That is fine. So long as you keep in mind which units you are using, you don't have to always convert to SI units.
The final velocity of hipster two is $v_{out,2} = 4158.39/100= 41.58$[km/h]. The deflection angle is obtained by \[ \phi_{def} = \tan^{-1}\!\!\left( \frac{ p_{out,2,y} }{ p_{out,2,x} } \right)= 32.76^\circ. \]
Discussion
We defined the concept of momentum in terms of the velocity of the object, but in fact, momentum is a more fundamental concept than velocity. If you go on to take more advanced physics classes, you will learn that the natural variables to describe the state of a particle are their positions and momenta $(\vec{x}, \vec{p})$. You will also learn that the real form of Newton's second law is written in terms of the momentum: \[ \vec{F} = \frac{d \vec{p} }{dt} \quad \text{for } m \text{ constant } \Rightarrow \quad \vec{F}=\frac{d (m\vec{v}) }{dt}=m\frac{d \vec{v} }{dt} =m\vec{a}. \] In most physics problems the mass of objects will stay constant so using $\vec{F}=m\vec{a}$ is perfectly fine.
The law of conservation of momentum follows from Newton's third law: for each force $\vec{F}_{12}$ exerted by Object 1 on Object 2, there exists a counter force $\vec{F}_{21}$ of equal magnitude and opposite direction, which is the force of Object 2 pushing back on Object 1. Earlier I said that it is difficult to quantify the magnitude of the exact forces $\vec{F}_{12}$ and $\vec{F}_{21}$ that occur during a collision. Indeed, the amount of force suddenly shoots up as the two objects collide and then suddenly drops. Complicated as these forces may be, we know that during the entire collision they obey Newton's third law. Assuming there are no other forces acting on the objects we have: \[ \vec{F}_{12} = -\vec{F}_{21} \quad \text{using the above} \Rightarrow \quad \frac{d \vec{p}_1 }{dt} = -\frac{d \vec{p}_2 }{dt}. \] If now move both terms to the left-hand side we obtain the equation: \[ \frac{d \vec{p}_1 }{dt} + \frac{d \vec{p}_2 }{dt} = \frac{d}{dt}\left( \vec{p}_1 + \vec{p}_2 \right) = 0, \] which implies that quantity $\vec{p}_1 + \vec{p}_2$ is constant over time.
In this section we saw how to use a momentum calculation to predict the motion of the particles after a collision. In the next section, we will learn about the concept of energy which is another useful concept for understanding and predicting the motion of objects.
Links
[ Animations of simple collisions between objects. ]
http://en.wikipedia.org/wiki/Conservation_of_linear_momentum
Energy
Instead of thinking about velocities $v(t)$ and motion trajectories $x(t)$, we can solve physics problems using energy calculations. In this section, we will define precisely the different kinds of energies that exist and then learn the rules of converting one energy into another. The key idea in this section is the principle of total energy conservation, which tells us that, in any physical process, the sum of the initial energies is equal to the sum of the final energies.
Example
Say you drop a ball from a height $h$[m] and you want to predict its speed right before it hits the ground. Using the kinematics approach, you would go for the general equation of motion: \[ v_f^2 = v_i^2 + 2a(y_f-y_i), \] and substitute $y_i=h$, $y_f=0$, $v_i=0$ and $a=-g$ to obtain the answer $v_f = \sqrt{2gh}$ for the final velocity at impact.
Alternately, you could use an energy calculation. Initially the ball starts from a height $h$, which means it has $U_i=mgh$[J] of potential energy. As the ball falls, the potential energy is converted into kinetic energy. Right before the ball hits the ground, it will have a final kinetic energy equal to the initial potential enegy: $K_f=U_i$ [J]. Since the formula for kinetic energy is $K=\frac{1}{2}mv^2$, we have $\frac{1}{2}mv_f^2 = mgh$. After cancelling the mass on both sides of the equation and solving for $v_f$ we obtain $v_f=\sqrt{2gh}$.
Both methods of solving the example problem come to the same conclusion, but the energy reasoning is arguably more intuitive than plugging values into a formula. In science, it is really important to know different ways for arriving at some answer. Knowing about these alternate routes will allow you to check your answers and to understand concepts better.
Concepts
Energy is measured in Joules [J] and it arises in several different contexts:
- $K =$ kinetic energy.
This is the type of energy that objects have by virtue of their motion.
- $W$ = work.
This is the amount of energy that an external
force adds or subtracts from a system. Positive work corresponds to energy being added to the system while negative work corresponds to energy being withdrawn from the system. * $U_g=$ **gravitational potential energy**. This is the energy that an object has by virtue of its position above the ground. We say this energy is //potential// because it is a form of //stored work//. The potential energy corresponds to the amount of work that the force of gravity will add to an object when you let the object fall to the ground. * $U_s= $ **spring potential energy.** This is the energy stored in a spring when it is displaced from its relaxed position. * There are many kinds other kinds of energy: electrical energy, magnetic energy, sound energy, thermal energy, etc. In this section, however, we limit out focus only on the //mechanical// energy concepts described above.
Formulas
Kinetic energy
An object of mass $m$ moving at velocity $\vec{v}$ has a kinetic energy of \[ K=\frac{1}{2}m\|\vec{v}\|^2 \qquad \text{[J]}. \] Note that the kinetic energy only depends on the speed $\|\vec{v}\|$ of the object and not the direction of motion.
Work
If an external force $\vec{F}$ acts on a object as it moves through a distance $\vec{d}$, the work done by this force is \[ W=\vec{F}\cdot \vec{d} = \|\vec{F}\| \|\vec{d}\|\cos \theta \qquad \text{[J]}, \] where the second equality follows from the geometrical interpretation of the dot product: $\vec{u}\cdot \vec{v} = \|\vec{u}\| \|\vec{v}\|\cos \theta$, with $\theta$ is the angle between $\vec{u}$ and $\vec{v}$.
If the force $\vec{F}$ acts in the same direction as the displacement $\vec{d}$, then it will do positive work ($\cos(180^\circ)=+1$)—the force will be adding energy to the system. If the force acts in the direction opposite to the displacement, then the work done will be negative ($\cos(180^\circ)=-1$), which means that energy is being withdrawn from the system.
Gravitational potential energy
An object raised to a height $h$ above the ground has a gravitational potential energy given by: \[ U_g(h) = mgh \qquad \text{[J]}, \] where $m$ is the mass of the object and $g=9.81$[m/s$^2$] is the gravitational acceleration on the surface of Earth.
Spring potential energy
The potential energy stored in a spring when it is displaced by $\vec{x}$[m] from its relaxed position is given by \[ U_{s} = \frac{1}{2}k\|\vec{x}\|^2 \qquad \text{[J]}, \] where $k$[N/m] is the spring constant.
Note that it doesn't matter whether the spring is stretched or compressed by a certain length: only the magnitude of the displacement matters $\|\vec{x}\|$.
Conservation of energy
Consider a system which starts from an initial state (i), undergoes some motion and arrives at a final state (f). The law of conservation of energy states that energy cannot be created or destroyed in any physical process. This means that the initial energy of the system plus the work that was input into the system must equal the final energy of the system plus any work that the was output: \[ \sum E_{i} \ \ + W_{in} \ \ \ = \ \ \ \sum E_{f} \ \ + W_{out}. \] The expression $\sum E_{(a)}$ corresponds to the sum of the different types of energy the system has in state (a). If we write down the equation in full we have: \[ K_i + U_{gi} + U_{si} \ \ \ + W_{in} \ \ \ = \ \ \ K_f + U_{gf} + U_{sf} \ \ \ + W_{out}. \] Usually, some of the terms in the above expression can be dropped. For example, we do not need to consider the spring potential energy $U_s$ in physics problems that do not involve springs.
Explanations
Work and energy are measured in Joules [J]. Joules can be expressed in terms of the fundamental units as follows: \[ [\text{J}] = [\text{N}\:\text{m}] = [\text{kg}\:\text{m}^2/\text{s}^{2}]. \] The first equality follows from the definition of work as force times displacement. The second equality comes from definition of the Newton [N]$=[\text{kg}\:\text{m}/\text{s}^2]$ via $F=ma$.
Kinetic energy
A moving object has energy $K=\frac{1}{2}m\|\vec{v}\|^2$[J], which we call kinetic energy from the Greek word for motion kinema.
Note that velocity $\vec{v}$ and speed $\|\vec{v}\|$ are not the same as energy. Suppose you have two objects of the same mass and one is moving twice faster than the other. The faster object will have twice the velocity, but four times more kinetic energy.
Work
When hiring someone to help you move, you have to pay them for the work they do. Work is the product of how much force is necessary for the move and the distance of the move. The more force, the more work there will be for a fixed displacement. The more displacement (think moving to the South Shore versus moving next door) the more money the movers will ask for.
The amount of work done by a force $\vec{F}$ on an object which moves along some path $p$ is given by: \[ W = \int_p \vec{F}(x) \cdot d\vec{x}, \] where we account for the fact that the magnitude and direction of the force might change throughout the motion.
If the force is constant and the displacement path is a straight line, the formula for work simplifies to: \[ W = \int_0^d \vec{F}\cdot d\vec{x} = \vec{F}\cdot\int_0^d d\vec{x} = \vec{F}\cdot \vec{d} = \|\vec{F}\|\|\vec{d}\|\cos\theta. \] Note the use of the dot product to obtain only the part of $\vec{F}$ that is pushing in the direction of the displacement $\vec{d}$. A force which acts perpendicular to the displacement produces no work, since it neither speeds up or slows down the motion.
Potential energy is stored work
Some kinds of work are just a waste of your time, like working in a bank for example. You work and you get your paycheque, but nothing remains with you at the end of the day. Other kinds of work leave you with some resource at the end of the work day. Maybe you learn something, or you network with a lot of good people.
In physics, we make a similar distinction. Some types of work, like work against friction, are called dissipative since they just waste energy. Other kinds of work are called conservative since the work you do is not lost: it is converted into potential energy.
The gravitational force and the spring force are conservative forces. Any work you do while lifting an object up into the air against the force of gravity is not lost but stored in the height of the object. You can get all the work/energy back if you let go of the object. The energy will come back in the form of kinetic energy since the object will pick up speed during the fall.
The negative of the work done against a conservative force is called potential energy. For any conservative force $\vec{F}_?$, we can define the associated potential energy $U_?$ through the formula: \[ U_?(d) = -W_{done} = - \int_0^d \vec{F}_? \cdot d\vec{x}. \] We will discuss two specific examples of this general formula below: the gravitational and spring potential energies. Being high in the air means you have a lot of potential to fall, and compressing a spring by a certain distance means it has the potential to spring back to its normal position. Let us look now at the exact formulas for these two cases.
Gravitational potential energy
The force of gravity is given by: \[ \vec{F}_g = -mg \hat{\jmath}. \] The direction of the gravitational force is downwards, towards the centre of the Earth.
The gravitational potential energy of lifting an object from a height of $y=0$ to a height of $y=h$ is given by: \[ \begin{align*} U_g(h) &\equiv - W_{done} \nl &= - \!\int_0^h \! \vec{F}_g \cdot d\vec{y} = - \!\int_0^h \!\!(-mg \hat{\jmath})\cdot \hat{\jmath} \; dy = mg \!\int_0^h \!\!\! 1\:dy = mg y\big\vert_{y=0}^{y=h} = mgh. \end{align*} \]
Spring energy
The force of a spring when stretched a distance $\vec{x}$[m] form its natural position is given by: \[ \vec{F}_s(\vec{x}) = - k\vec{x}. \]
The potential energy stored in a spring as it is compressed from $y=0$ to $y=x$[m] is given by: \[ \begin{align*} U_s(x) &= -W_{done} \nl &=-\!\int_0^x \!\vec{F}_{s}(y) \cdot d\vec{y} = \int_0^x \!\! ky dy = k\int_0^x \!\! y dy = k\frac{1}{2}y^2\big\vert_{y=0}^{y=x} = \frac{1}{2}kx^2. \end{align*} \]
Conservation of energy
Energy cannot be created or destroyed. It can only be transforms from one form to another. If there are no external forces acting on the system, then we have conservation of energy: \[ \sum E_i \ \ = \ \ \sum E_f. \]
If there are external forces like friction that do work on the system, we must take their energy contributions into account as well: \[ \sum E_i \ +\ W_{in} = \sum E_f, \quad \text{or} \quad \sum E_i = \sum E_f \ +\ W_{out}. \]
This is one of the most important equations you will find in this book, because it will allow you to solve very complicated problems simply by accounting for all the different kinds of energy involved in the problem.
Examples
Banker dropped
An investment banker is dropped (from rest) from a 100[m] tall building. What is his speed when he hits the ground?
We start from: \[ \begin{align*} \sum E_i \ \ &= \ \ \sum E_f, \nl K_i + U_i \ \ & = \ \ K_f + U_f, \end{align*} \] and plugging in the numbers we get: \[ 0 + m \times9.81 \times100 = \frac{1}{2}mv^2 + 0. \] After cancelling the mass $m$ from both sides of the equation we are left with \[ 9.81\times 100 = \frac{1}{2}v_f^2. \] Solving for $v_f$ in the above equation, we find that the banker will be going at $v_f =\sqrt{ 2\times 9.81\times 100}=44.2945$[m/s] when he hits the ground. This is like $160$[km/h]. Ouch! That will definitely hurt.
Bullet speedometer
 An incoming bullet at speed $v$ hits a mass $M$ suspended on two strings.
Use conservation of momentum and conservation of energy principles to
find the speed $v$ of the bullet if the block rises to a height $h$ after
it is hit by the bullet.
An incoming bullet at speed $v$ hits a mass $M$ suspended on two strings.
Use conservation of momentum and conservation of energy principles to
find the speed $v$ of the bullet if the block rises to a height $h$ after
it is hit by the bullet.
First we use the conservation of momentum principle to find the (horizontal) speed of the block and mass right after the bullet hits: \[ \vec{p}_{in,m} + \vec{p}_{in,M} = \vec{p}_{out}, \] \[ m v + 0 = (m+M) v_{out}, \] so the velocity of the block with the bullet embedded in it is $v_{out}= \frac{mv}{M+m}$ right after collision.
Next we use the conservation of energy principle to relate the initial kinetic energy of the block-plus-bullet and the height $h$ by which it rises: \[ K_i + U_i = K_f + U_f, \] \[ \frac{1}{2}(M+m)v_{out}^2 + 0 = 0 + (m+M)gh. \] Isolating $v_{out}$ in the above equation and setting it equal to the $v_{out}$ we got from the momentum calculation we get: \[ v_{out} = \frac{mv}{M+m} = \sqrt{2gh} = v_{out}. \] We can use this equation to find the speed of the incoming bullet: \[ v = \frac{M+m}{m}\sqrt{2gh}. \]
Incline and spring
A block of mass $m$ is released from rest at point (A) on the top of an incline at a coordinate $y=y_i$. It slides down the frictionless incline to the point (B) $y=0$. The coordinate $y=0$ corresponds to the relaxed length of a spring of spring constant $k$. The block then compresses the spring all the way to point (C ), corresponding to $y=y_f$, when the block comes to rest again. The angle of the slope is $\theta$.
What is the speed of the block at $y=0$? How far does the spring get compressed $y_f$? Bonus points if you can express your answer for $y_f$ in terms of $\Delta h$, the difference in height between $y_i$ and $y_f$.
We have essentially two problems: the motion from (A) to (B) in which the gravitational potential energy of the block is converted into kinetic energy and the motion from (B) to (C ) in which the all the energy of the block gets converted into spring potential energy.
In both cases, there is no friction so we can use the conservation of energy formula: \[ \sum E_i \ \ = \ \ \sum E_f. \]
For the motion from (A) to (B) we have: \[ K_i + U_i = K_f + U_f. \] The block starts from rest so $K_i=0$. The difference in potential energy is equal to $mgh$ and in this case the block is $|y_i|\sin\theta$ [m] higher at (A) than it is at (B), so we can write: \[ 0 + mg|y_i|\sin\theta = \frac{1}{2}mv_B^2 + 0. \] The above formula uses the point (B) at $y=0$ as reference for the gravitational potential energy. The potential at point (A) is $U_i=mgh=mg|y_i-0|\sin\theta$ relative to point (B) since the point (A) is $h=|y_i-0|\sin\theta$ metres higher than the point (B).
Solving for $v_B$ in this equation gives us the answer to the first part of the question: \[ v_{B} = \sqrt{ 2 g|y_i|\sin\theta }. \]
Now for the second part of the motion. The law of conservation of energy dictates that: \[ K_i + U_{gi} + U_{si} = K_f + U_{gf} + U_{sf}, \] where now $i$ refers to the moment (B) and $f$ refers to the moment (C ). Initially the spring is uncompressed so $U_{si}=0$, and by the end of the motion the spring is compressed by a total of $\Delta y=|y_f-0|$[m], so its spring potential energy is $U_{sf}=\frac{1}{2}k|y_f|^2$. We choose the height of (C ) as the reference potential energy and thus $U_{gf}=0$. Since the difference in gravitational potential energy is $U_{gi} - U_{gf}=mgh=|y_f-0|\sin\theta$, we can fill-in the entire energy equation: \[ \frac{1}{2}m v_B^2 + mg|y_f|\sin\theta + 0 = 0 + 0 + \frac{1}{2}k|y_f|^2. \] Since $k$ and $m$ are given and we know $v_B$ from the first part of the question, we can solve for $|y_f|$ (a quadratic equation).
To obtain the answer $|y_f|$ in terms of $\Delta h$ we can use $\sum E_i = \sum E_f$ again, but this time $i$ will refer moment (A) and $f$ refers to the moment (C ). The energy equation becomes $mg\Delta h = \frac{1}{2}k|y_f|$ from which we obtain $|y_f|=\frac{ 2 mg\Delta h}{k}$.
Energy lost to friction
You have a block of mass 50[kg] on an incline. The force of friction between the block and the incline is 30N. The block slides for 200[m] down the incline. The incline is at a slope $\theta=30^\circ$ so the total vertical displacement of the block is $200\sin30=100$[m]. What is its speed as it reaches the bottom of the incline?
This is a problem in which initial energies are converted into final energies and some lost work: \[ \sum E_i = \sum E_f + W_{lost}. \] The term $W_{lost}$ represents the energy lost due to the friction.
Another (better) way of describing the situation is that the block had a negative amount of word done on it \[ \sum E_i + \underbrace{W_{done}}_{ \textrm{negative} } = \sum E_f. \] The quantity $W_{done}$ is negative because during the entire motion the friction force on the object was acting in the opposite direction to the motion: \[ W_{done} = \vec{F}\cdot \vec{d} = \|\vec{F}_f\|\|\vec{d}\|\cos(180^\circ) = - F_f\|\vec{d}\|, \] where $\vec{d}$ is the $200$[m] of sliding distance during which the friction acts. Since we are told that $F_f = 30$[N], we can calculate $W_{done} = W_{friction} = -30[\text{N}]\times 200[\text{m}] = -6000$[J].
We can now substitute this value into the conservation of energy equation: \[ \begin{align*} K_i + U_i + W_{done} &= K_f + U_f, \nl 0 + mgh + (-F_f|d|) &= \frac{1}{2}mv_f^2 + 0, \end{align*} \] where we have used the formula $mgh= U_i- U_f$ for the difference in gravitational potential energy. Substituting all the values we know we get \[ 0 + 50 \times 9.81 \times 100 - 6000 = \frac{1}{2}(50)v_f^2 + 0, \] which can be solved for $v_f$.
Discussion
In this section we saw that describing physical situation in terms of the energies involved is a useful way of thinking. The law of conservation of energy allows us to do simple “energy accounting” and calculate the values of unknown quantities.
Uniform circular motion
In this section we will learn about the circular motion of objects. Circular motion is different from linear motion and we will have to develop new techniques and concepts which are better suited for the description of circular motion.
Imagine a rock of mass $m$ is swinging around in a horizontal circle attached at the end of a rope. The rock is flying through the air at a constant (uniform) speed of $v_t$[m/s] along a circular path of radius $R$[m] at a height $h$[m] above the ground. What is the tension $T$ in the rope?
Consider a coordinate system which has the $x$ and $y$ axis placed on the ground level at the centre of the circle of motion are the $z$ axis measuring the height above the ground. In that coordinate system, the trajectory of the rock is described by the equation \[ \vec{r}(t) =(x(t),y(t),z(t)) = \left(R\cos\!\left(\frac{v_t}{R}\:t\right),\ R\sin\!\left(\frac{v_t}{R}\:t\right), \ h\right). \] You will agree with me that this expression looks somewhat complicated. This complexity stems from the fact that the $(x,y,z)$ coordinate system is not very well adapted for the description of circular paths.
A new coordinate system
Instead of the usual coordinate system $\hat{x},\hat{y},\hat{z}$ which is static, we can use a new coordinate system $\hat{t},\hat{r},\hat{z}$ that is “attached” to the rotating object.
Three important directions can be identified:
- $\hat{t}$: the tangential direction in the instantaneous direction of motion of the object.
The name comes from the Greek word for “touch” (imagine a straight line “touching” the circle).
- $\hat{r}$: the radial direction always points towards the centre of the circle of rotation.
- $\hat{z}$: the usual $\hat{z}$ direction, which is perpendicular to the plane of rotation.
From the point of view of a static observer, the tangential and radial directions constantly change their orientation as the object rotates around in a circle. From the point of view of the rotating object, the tangential and radial directions are fixed. The tangential direction is always “forward” and the radial direction is always to the side.
We can use the new coordinate system to describe the position, velocity and acceleration of the object undergoing circular motion:
- $\vec{v}=(v_r,v_t)_{\hat{r}\hat{t}}$: the velocity of object expressed with respect to
the $\hat{r}\hat{t}$ coordinates.
- $\vec{a}=(a_r,a_t)_{\hat{r}\hat{t}}$: The acceleration of the object in the $\hat{r}\hat{t}$ coordinates.
The most important parameters of motion are the tangential velocity $v_t$, the radial acceleration $a_r$ and the radius of the circle of motion $R$. We have $v_r=0$ since the motion is entirely in the $\hat{t}$ direction, and $a_t=0$ because we assumed that the tangential velocity $v_t$ remains constant (uniform circular motion).
In the next section we will learn how to calculate the radial acceleration $a_r$.
Radial acceleration
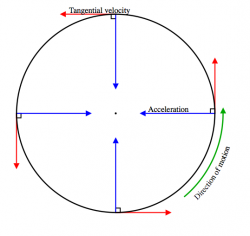 The defining feature of circular motion is the presence of an acceleration
that acts perpendicularly to direction of motion.
At each instant, the object wants to continue moving along the tangential direction,
but the radial acceleration causes the velocity to change direction.
The result of this constant inward acceleration is that the object will
follow a circular path.
The defining feature of circular motion is the presence of an acceleration
that acts perpendicularly to direction of motion.
At each instant, the object wants to continue moving along the tangential direction,
but the radial acceleration causes the velocity to change direction.
The result of this constant inward acceleration is that the object will
follow a circular path.
The radial acceleration $a_r$ of an object moving in a circle of radius $R$ with a tangential velocity $v_t$ is given by: \[ a_r = \frac{v^2_t}{ R }. \] This is an important equation which relates the three key parameters of circular motion.
According to Newton's second law $\vec{F}=m\vec{a}$, the radial acceleration of the object must be caused by a radial force. We can calculate the magnitude of this radial force $F_r$ as follows: \[ F_{r} = ma_r = m \frac{v^2_t}{ R }. \] The above formula allows us to connect the observable aspects of the circular motion $v_t$ and $R$ with its cause: the force $F_r$ which always acts towards the centre of rotation.
To put it differently, we can say that circular motion requires a radial force. From now on, every time you see an object undergoing circular motion, you should try to visualize the radial force which is causing the circular motion.
In the rock-on-a-rope example described in the beginning of this section, the circular motion was caused by the tension of the rope which always acts in the radial direction (towards the centre of rotation). We are now in a position to calculate the value of the tension $T$ in the rope using the equation: \[ F_{r} = T = ma_r, \qquad \Rightarrow \qquad T=m \frac{v^2_t}{ R }. \]
Example
During a student protest, a young activist called David is stationed on the rooftop of a building of height $12$[m]. A mob of blood-thirsty neoconservatives is slowly approaching his position determined to lynch him because of his leftist views. David has put together a make-shift weapon by attaching a 0.3[kg] rock to the end of a shoelace of length $1.5$[m]. The maximum tension that the shoelace can support is 500[N]. What is the maximum tangential velocity $\max\{v_t\}$ that the shoelace can support? What is the maximum range for this projectile when it is launched from the roof?
The first part of the question is answered easily using the $T=m \frac{v^2_t}{ R }$ formula: $\max\{v_t\} = \sqrt{ \frac{R T}{m} }= \sqrt{ \frac{1.5\times 500}{0.3} }=50$[m/s]. To answer the second question, we must solve for the distance travelled by a projectile with initial velocity $\vec{v}_i=(v_{ix},v_{iy})=(50,0)$[m/s] launched from $\vec{r}_i=(x_i,y_i)=(0,12)$[m]. First we solve for the total time of flight $t_f=\sqrt{2\times 12/9.81}=1.56$[s]. Then we find the range by multiplying this time by the horizontal speed $x(t_f)=0+v_{ix} t_f = 50\times 1.56=78.20$[m].
After carrying out these calculations on a piece of paper, David starts to spin-up the rock and waits for the neocons to come into range.
Circular motion parameters
We now introduce some further terminology used to describe circular motion:
- $C=2\pi R$[m]: The circumference of the circle of motion.
- $T$: The period of the motion is how long it takes for the object to complete one full circle.
The period is measured in seconds [s].
- $f=\frac{1}{T}$: The frequency of rotation. How many times per second does the object pass by
some reference point on the circle. Frequency is measured in Hertz [Hz]=[1/s].
We sometimes describe the frequency of rotation in //revolutions per minute// (RPM).
* $\omega\equiv\frac{v_t}{R}=2\pi f$: The //angular velocity// describes how fast the
object is rotating. Angular velocity is measured in [rad/s].
Recall that a circle of radius $R$ has circumference $C = 2 \pi R$. The period $T$ is defined as how long it will take the object to complete one full turn around the circle: \[ T = \frac{\text{distance}}{\text{speed}} = \frac{C}{v_t} = \frac{2\pi R}{v_t}, \] where $C=2\pi R$ is total distance that must be travelled to compete one turn and $v_t$ is the velocity of the object along the curve. The object will complete one full turn every $T$ seconds.
Another way of describing the motion is to talk about the frequency: \[ f=\frac{1}{T} = \text{[Hz]}. \] The frequency tells you how many turns the object completes in one second. If the object competes one turn in $T=0.2$[s], then the motion has frequency $f=5$[Hz], or $f=60\times 5 = 300$[RPM].
The most natural parameter for describing rotation is in terms of the angular velocity $\omega$[rad/s]. We know that one full turn corresponds to an angle of rotation of $2\pi$[rad], so the angular velocity is obtained by dividing $2\pi$ by the time it takes to complete one turn: \[ \omega = \frac{2\pi}{T} = 2\pi f = \frac{v_t}{R}. \]
The angular velocity $\omega$ is very useful because it describes the speed of the circular motion without any reference to the radius. If we know that the angular velocity of an object is $\omega$, we can obtain the tangential velocity by multiplying times the radius: $v_t=R\omega$[m/s].
Let us now look at some examples in which we are asked to compute some angular velocities.
Bicycle odometer
Imagine that you place a small speed detector gadget on one of the spokes of the front wheel of your bicycle. Your bike's wheels have a radius $R=14$[in] and the gadget is attached at a distance of $\frac{3}{4}R$[m] from the centre of the wheel. Find the angular velocity $\omega$, period $T$, and frequency $f$ of rotation for the wheel when the speed of the bicycle relative to the ground is $40$[km/h]. What is the tangential velocity $v_t$ of the detector gadget?
The velocity of the bicycle relative to the ground $v_{bike}=40$[km/h] is equal to the tangential velocity of the rim of the wheel: \[ v_{bike} = v_{rim} = 40 [\text{km/h}] \times \frac{ 1000 [\text{m}] }{ 1 [\text{km}]} \times \frac{ 1 [\text{h}] }{ 3600 [\text{s}]} = 11.11 [\text{m/s}]. \] We can find the angular velocity using $\omega = \frac{v_{rim}}{R}$ and the radius of the wheel $R=14[\text{in}]=0.355$[m]. We obtain $\omega = \frac{11.11}{0.355}= 31.24[\text{rad/s}]$. From this we can easily calculate $T=\frac{2\pi}{\omega}=0.20$[s] and $f=\frac{1}{0.20}=5$[Hz]. Finally, to compute the tangential velocity of the gadget we multiply the angular velocity $\omega$ by its radius of rotation to obtain $v_{det}= \omega \times \frac{3}{4}R = 8.333$[m/s].
Rotation of the Earth
It takes exactly 23 hours, 56 minutes and 4.09 seconds for the Earth to compete one full turn ($2\pi$ radians) around its axis of rotation. What is its angular velocity? What is the tangential speed at a latitude of $45^\circ$ (Montreal)?
We can find $\omega$ by carrying out a simple conversion: \[ \frac{2\pi \text{ [rad]}}{ 1 \text{ [day]} } \cdot \frac{1 \text{ [day]}}{ 23.93447 \text{ [h]} } \cdot \frac{1 \text{ [h]}}{ 3600 \text{ [s]} } = 7.2921\times 10^{-5} \text{ [rad/s]}. \]
The radius of the trajectory traced out by someone at a latitude of $45^\circ$ (Montreal) is given by $r=R\cos(45^\circ)=4.5025\times 10^6$[m], where $R=6.3675×10^6$[m] is the radius of the Earth. Thus, though it may seem that you are not moving right now, in reality you are hurtling through space at a speed of \[ v_t = r \omega = 4.5025\times 10^6 \times 7.2921\times 10^{-5} = 464.32 \text{ [m/s]}. \] Which is $1671.56$[km/h]. Just try to imagine that for a second. You can try to use this fact if you get stopped by the cops one day for a speeding infraction: “Yes officer, I was doing 130[km/h], but this is really a negligible speed relative to the 1671[km/h] that the Earth is doing around the sun.”
Three dimensions
For some problems involving circular motion, it will be necessary to consider the $z$ direction in the force diagram. The best approach in this case is to draw the force diagram as a cross section, which is perpendicular to the tangential direction. The diagram will show the $\hat{r}$ and $\hat{z}$ axes.
Using the force diagram, you should be able to find all the forces in the radial and vertical directions and solve for accelerations $a_r$, $a_z$. Remember that you can always use the relation $a_r=\frac{v_t^2}{R}$ which connects the value of $a_r$ with the tangential velocity $v_t$ and the radius of rotation $R$.
Example
Japanese people of the future want to design a giant racetrack for retired superconducting speed trains. The shape of the race track is a big circle with radius $R=3$[km]. Because the trains are magnetically levitated, there is no friction between the track and the train $\mu_s=0, \mu_k=0$. What is the bank angle required for the race track so that trains moving at a speed of exactly $400$[km/h] will stay on the track without moving laterally?
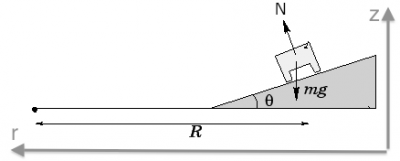 We begin by drawing a force diagram which shows a cross-cut of the
train in the $\hat{r}$ and $\hat{z}$ directions.
The bank angle of the racetrack is $\theta$. This is the unknown we are looking for.
Because of the frictionless-ness of levitated superconducting suspension
there cannot be any force of friction $F_f$ so the only forces on the
train will be it weight $\vec{W}$ and the normal force $\vec{N}$.
We begin by drawing a force diagram which shows a cross-cut of the
train in the $\hat{r}$ and $\hat{z}$ directions.
The bank angle of the racetrack is $\theta$. This is the unknown we are looking for.
Because of the frictionless-ness of levitated superconducting suspension
there cannot be any force of friction $F_f$ so the only forces on the
train will be it weight $\vec{W}$ and the normal force $\vec{N}$.
The next step is to write down the force equations for the two directions: \[ \begin{align*} \sum F_r &= N\sin\theta = m a_r = m \frac{v_t^2}{R} \quad \Rightarrow \quad N\sin\theta = m \frac{v_t^2}{R}, \nl \sum F_z &= N\cos\theta - mg = 0 \ \ \quad \quad \Rightarrow \quad N\cos\theta = mg. \end{align*} \] Note how the normal force $\vec{N}$ is split into two parts: the vertical component counter balances the weight of the train, while the component in the $\hat{r}$ direction is the force that is responsible for causing the rotational motion of the train around the track.
We want to solve for $\theta$ in the above equations. A commonly used trick for solving equations containing multiple trigonometric functions is to divide one equation by the other. We obtain: \[ \frac{ N \sin\theta }{ N\cos\theta } =\frac{ m \frac{v_t^2}{R} }{ mg} \quad \Rightarrow \quad \tan\theta = \frac{ v_t^2 }{ Rg }. \] The final answer is $\theta = \tan^{-1}\!\!\left(\frac{v_t^2}{gR} \right) = \tan^{-1}\!\!\left(\frac{(400\times\frac{1000}{3600})^2}{9.81 \times 3000} \right) = 22.76^\circ$. If the angle were any steeper, the trains would fall towards the centre. If the bank angle were any shallower, the trains would fly off to the side. The angle $22.76^\circ$ is just right.
Discussion
Radial acceleration
In the kinematics section we studied problems involving linear acceleration: in which an acceleration $a$ was acting in the same direction as the velocity and was thus causing a change the magnitude of the velocity $v$.
Circular motion deals with a different situation in which the speed $\|\vec{v}\|$ of the object remains constant but the velocity $\vec{v}$ changes direction. At each point along the circle, the velocity of the object points along the tangential direction and during each instant the radial acceleration pulls the object inwards and causes it to rotate.
Another term for radial acceleration is centripetal acceleration, which literally means “tending towards the centre”.
Centrifugal force
When a car makes a left turn, the passenger riding shotgun will feel pushed towards the right: into the passenger door. Some people erroneously attribute this effect to a centrifugal force, which acts away from the centre of rotation. During a sharp turn, these people feel as though they are being flung out of the car and therefore they conclude that there must be some force which is responsible for this.
The reason why we feel as though we are being thrown out of the car is due to Newton's first law which says that, in the absence of external forces, an object will continue moving in a straight line. Since your initial motion is in the $\hat{t}$ direction, your body will naturally continue moving in that direction because of Newton's first law. The force of the car door pushes you inwards and keeps you in the circular trajectory. If it weren't for the door, you would fly straight on.
Radial forces do no work
An interesting property of radial forces is that they do zero work. Recall that the work done by a force $\vec{F}$ during a displacement $\vec{d}$ is computed using the dot product $W=\vec{F}\cdot \vec{d}$. For circular motion, the displacement is always in the $\hat{t}$ direction, whereas the radial force is in the $\hat{r}$ direction so the dot product of the two is zero.
This is why it is possible for the speed of the object undergoing circular motion to remain constant despite the fact that it is being accelerated. The effects of the radial acceleration do not increase the speed: they only act to change the direction of the velocity.
Exercises
Staying in touch
 A vertical loop of radius 5[m] is placed on a racetrack.
What is the minimum speed $v$ for a motorcyclist to come into
the loop and make it around? The motorcyclist will “lose contact” with the top of the ramp if the magnitude of the normal force becomes zero.
A vertical loop of radius 5[m] is placed on a racetrack.
What is the minimum speed $v$ for a motorcyclist to come into
the loop and make it around? The motorcyclist will “lose contact” with the top of the ramp if the magnitude of the normal force becomes zero.
Solution. Find $v_{top}$ when $\vec{N}=0$ and then use conservation of energy to find $v$ in terms of $v_{top}$. Ans: $v=\sqrt{5g+20g}=5\sqrt{g}$.
Links
[ Banked curve exercise ]
http://www.chaostoy.com/cd/html/banked_e.htm
Angular motion
We will now study the physics of objects in rotation. A simple example of this kind of motion is a rotating disk. Other examples include rotating bicycle wheels, spinning footballs and spinning figure skaters.
As you will see shortly, the basic concepts used to describe angular motion are directly analogous to the concepts for linear motion: position, velocity, acceleration, force, momentum and energy.
Review of linear motion
It is instructive to begin our discussion with a brief review of the concepts and formulas used to describe the linear motion of objects.
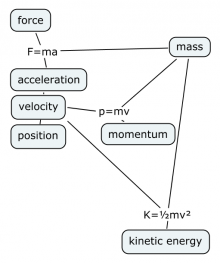 The linear motion of an object is described by its position $x(t)$,
velocity $v(t)$ and acceleration $a(t)$ as functions of time.
The position function tells you where the object is,
the velocity tells you how fast it is moving and
the acceleration measures the change in the velocity of the object.
The linear motion of an object is described by its position $x(t)$,
velocity $v(t)$ and acceleration $a(t)$ as functions of time.
The position function tells you where the object is,
the velocity tells you how fast it is moving and
the acceleration measures the change in the velocity of the object.
The motion of objects is governed by Newton's first and second laws. In the absence of external forces, objects will maintain a uniform velocity (UVM) which corresponds to the equations of motion: $x(t)=x_i+v_it$, $v(t)=v_i$. If there is a net force $\vec{F}$ acting on the object, the force will cause the object to accelerate and the magnitude of the acceleration is obtained using the formula $F=ma$. A constant force acting on an object will produce a constant acceleration (UAM), which corresponds to the equations of motion: $x(t)=x_i+v_it+\frac{1}{2}at^2$, $v(t)=v_i + at$.
We also learned how to quantify the momentum $\vec{p}=m\vec{v}$ and the kinetic energy $K=\frac{1}{2}mv^2$ of moving objects. The momentum vector is the natural measure of the “quantity of motion,” which plays a key role in collisions. The kinetic energy measures how much energy the object has by virtue of its motion.
The mass of the object $m$ is an important factor in many of the equations of physics. In the equation $F=ma$, the mass $m$ measures the objects inertia, i.e., how much resistance the object offers to being accelerated. The mass of the object also appears in the formulas for momentum and kinetic energy: the heavier the object is, the larger its momentum and its kinetic energy will be.
Concepts
We now introduce the new concepts used to describe the angular motion of objects.
- The kinematics of rotating objects is described in terms of angular quantities:
- $\theta(t)$[rad]: The angular position.
- $\omega(t)$[rad/s]: The angular velocity.
- $\alpha(t)$[rad/s$^2$]: The angular acceleration.
- $I$[kg m$^2$]: The moment of inertia of an object tells you how difficult it is to make it turn.
The quantity $I$ plays the same role in angular motion as the mass $m$ plays in linear motion.
- $\mathcal{T}$[N$\:$m]: The torque is a measures angular force.
Torque is the cause of angular acceleration.
The angular equivalent of Newton's second law $\sum F=ma$ is given by the equation
$\sum\mathcal{T}=I\alpha$.
In words, this law states that applying an angular force (torque) $\mathcal{T}$
will produce an amount of angular acceleration $\alpha$ which is
inversely proportional to the moment of inertia $I$ of the object.
* $L=I\omega$[kg$\:$m$^2$/s]: The //angular momentum// of a rotating object describes
the "quantity of spinning stuff."
* $K_r=\frac{1}{2}I\omega^2$[J]: The //angular// or //rotational// kinetic energy
quantifies the amount of energy an object has by virtue of its rotational motion.
Formulas
Angular kinematics
Instead of talking about position $x$, velocity $v$ and acceleration $a$, we will now talk about the angular position $\theta$, angular velocity $\omega$ and angular acceleration $\alpha$. Except for this change of ingredients, the recipe for fining the equations of motion remains the same: \[ \alpha(t) \ \ \overset{\omega_i + \int\!dt}{\longrightarrow} \ \ \omega(t) \ \ \overset{\theta_i+ \int\!dt }{\longrightarrow} \ \ \theta(t). \] Given the knowledge of the angular acceleration $\alpha(t)$, the initial velocity $\omega_i$ and the initial position $\theta_i$, we can use integration in order to find the equation of motion $\theta(t)$ which describes the angular position of the rotating object at all times.
Though this recipe can be applied to any form of angular acceleration function, you are only required to know the equations of motion for two special cases: the case of constant angular acceleration $\alpha(t)=\alpha$ and the case of zero angular acceleration $\alpha(t)=0$. These are the angular analogues of uniform acceleration motion and uniform velocity motion which we studied in the kinematics section.
The equations which describe uniformly accelerated angular motion are: \[ \begin{align*} \alpha(t) &= \alpha, \nl \omega(t) &= \alpha t + \omega_i, \nl \theta(t) &= \frac{1}{2}\alpha t^2 + \omega_it + \theta_i, \nl \omega_f^2 &= \omega_i^2 + 2\alpha(\theta_f - \theta_i). \end{align*} \] Note how the form of the equations is identical to the UAM equations. This should come as no surprise since the both sets of equations are obtained from the same integrals.
The equations of motion for uniform velocity angular motion are: \[ \begin{align*} \alpha(t) &= 0, \nl \omega(t) &= \omega_i, \nl \theta(t) &= \omega_it + \theta_i. \end{align*} \]
Relation to linear quantities
The angular quantities $\theta$, $\omega$ and $\alpha$ are the natural parameters for describing the motion of rotating objects. In certain situations, however, we may want to relate the angular quantities to linear quantities like distance, velocity and linear acceleration. This can be accomplished by multiplying the angular quantity by the radius of motion: \[ d = R\theta, \quad v = R\omega, \quad a = R\alpha. \]
For example, suppose you have a spool of network cable with radius 20[cm] and you need to measure out a length of 20[m] so as to connect your computer to your neighbours' computer. How many turns from the spool will you need? To find out, we can solve for $\theta$ in the formula $d=R\theta$ and obtain $\theta = 20/0.2=100$[rad] which corresponds to 15.9 turns.
Torque
Torque is angular force. In order to make an object rotate, you must exert a torque on it. Torque is measured in Newton metres [N$\:$m].
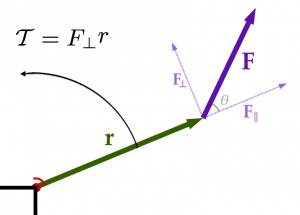 The torque produced by a force depends on how far from the centre of rotation it is applied:
\[
\mathcal{T} = F_{\!\perp}\: r = \|\vec{F}\|\sin\theta\; r,
\]
where $r$ is called the leverage.
Note that only the $F_{\perp}$ component of the force creates a torque.
The torque produced by a force depends on how far from the centre of rotation it is applied:
\[
\mathcal{T} = F_{\!\perp}\: r = \|\vec{F}\|\sin\theta\; r,
\]
where $r$ is called the leverage.
Note that only the $F_{\perp}$ component of the force creates a torque.
To understand the meaning of the torque equation, you should stop reading right now and go experiment with a door. If you push the door close to the hinges, it will take a lot more force to make it move than if you push far from the hinges. The more leverage $r$ you have, the more torque you will produce. Also, if you pull on the door handle away from the hinges, your force will have only a $F_{||}$ component so no matter how hard you pull, you will not cause the door to move.
The standard convention is to call torques that produce counter-clockwise motion positive and torques that cause clockwise rotation negative.
The relationship between torque and force can also be used in the other direction. If an electric motor produces a torque of $\mathcal{T}$[N$\:$m] and is attached to a chain wheel of radius $R$ then the tension in the chain will be: \[ T = F_{\perp} = \mathcal{T}/R \qquad [\text{N}]. \] Using this equation, you could compute the maximum pulling force produced by your car. You will have to lookup the value of the maximum torque produced by your car's engine and then divide by the radius of your wheels.
Moment of inertia
The momentum of inertia of an object describes how difficult it is to make the object rotate: \[ I = \{ \text{ how difficult it is to make an object turn } \}. \]
The calculation of the moment of inertia takes into account the mass distribution of the object. An object which has most of its mass close to the centre will have a smaller moment of inertia, whereas objects which have their mass far from the centre will have a large moment of inertia.
The formula for calculating the moment of inertia is: \[ I = \sum m_i r_i^2 = \int_{obj} r^2 \; dm \qquad [\text{kg}\:\text{m}^2]. \] The above equation indicates that we need to weight each part of the object by the squared distance of that part from the centre, hence the units $[\text{kg}\:\text{m}^2]$.
We rarely calculate the moment of inertia of objects using the above formula. Most of the physics problems you will have to solve will involve geometrical shapes for which the moment of inertia is given by simple formulas: \[ I_{disk} = \frac{1}{2}mR^2, \quad I_{ring}=mR^2, \] \[ I_{sphere} = \frac{2}{5} mR^2, \quad I_{sph. shell} = \frac{2}{3} mR^2. \] When you learn more about calculus, you will be able to derive each of the above formulas on your own. For now, just try to remember the formulas for the inertia of the disk and the ring as they are likely to come up in problems.
The quantity $I$ plays the same role in the equations of angular motion as the mass $m$ plays in the equations of linear motion.
Torques cause angular acceleration
Recall Newton's second law $F=ma$ which describes the amount of acceleration produced by a given force acting on an object. The angular analogue of Newton's second law is the following equation: \[ \mathcal{T} = I \alpha. \] This equation indicates that the angular acceleration produced by the a toque $\mathcal{T}$ is inversely proportional to the object's moment of inertia. Torque is the cause of angular acceleration.
Angular momentum
The angular momentum of a spinning object measures the “amount of rotational motion” that the object has. The formula for the angular momentum of a an object with moment of inertia $I$ rotating at an angular velocity $\omega$ is: \[ L = I \omega \qquad [\text{kg}\:\text{m}^2/\text{s}]. \]
The angular momentum of an object is a conserved quantity in the absence of external torques: \[ L_{in} = L_{out}. \] This is similar to the way momentum $\vec{p}$ is a conserved quantity in the absence of external forces.
Rotational kinetic energy
The kinetic energy of a rotating object is calculated as follows: \[ K_r = \frac{1}{2} I \omega^2 \qquad [\text{J}]. \] This is the rotational analogue to the linear kinetic energy $\frac{1}{2}mv^2$.
The amount of work produced by a torque $\mathcal{T}$ which is applied during an angular displacement of $\theta$ is given by: \[ W = \mathcal{T}\theta \qquad [\text{J}]. \]
Using the above equations, we can now include the energy and work associated with rotational motion into conservation of energy calculations.
Examples
Rotational UVM
A disk is spinning at a constant angular velocity of $12$[rad/s]. How many turns will the disk complete in one minute?
Since the angular velocity is constant, we can use the equation $\theta(t) = \omega t + \theta_i$ to find the total angular displacement after one minute. We obtain $\theta(60)=12\times 60=720$[rad]. To obtain the number of turns, we divide this number by $2\pi$ and obtain 114.6[turns].
Rotational UAM
A solid disk of mass $20$[kg] and radius $30$[cm] is initially spinning with an angular velocity of $20$[rad/s]. A brake pad applied to the edge of the disk produces a friction force of 60[N]. How long before the disk stops?
To solve the kinematics problem, we need to find the angular acceleration produced by the brake. We can do this using the equation $\mathcal{T}=I\alpha$. We must find $\mathcal{T}$ and $I_{disk}$ and solve for $\alpha$. The torque produced by the brake is calculated using the force-times-leverage formula: $\mathcal{T}=F_{\perp}r= 60\times 0.3=18$[N$\:$m]. The moment of inertia of a disk is given by $I_{disk} = \frac{1}{2}mR^2=\frac{1}{2}(20)(0.3)^2=0.9$[kg m$^2$]. Thus we have $\alpha=20$[rad/s$^2$]. We can now use the UAM formula for the angular velocity $\omega(t) = \alpha t + \omega_i$ and solve for the time when the motion will stop: $0 = \alpha t + \omega_i$. The disk will come to a stop after $t=\omega_i/\alpha = 1$[s].
Combined motion
A pulley of radius $R$ and moment of inertia $I$ has a rope wound around it and a mass $m$ attached at the end of the rope. What will be the angular acceleration of the disk if we let the mass drop to the ground while unwinding the rope.
A force diagram on the mass tells us that $mg-T=ma_y$ (where $\hat{y}$ points downwards). The torque diagram on the disk tells us that $TR = I \alpha$. Adding $R$ times the first equation to the second we get: \[ R({mg - T}) + T R = R m a_y + I \alpha, \] or after simplification we get: \[ R m g = R m a_y + I \alpha. \] But we know that the rope forms a solid connection between the disk and the mass block, so we must also have $R \alpha = a_y$, so if we substitute for $a_y$ we get: \[ R m g = R m R \alpha + I \alpha = (R^2 m + I) \alpha. \] Solving for $\alpha$ we obtain: \[ \alpha = \frac{ R m g }{ R^2 m + I }. \] This answer makes sense intuitively. The numerator is the “cause” of the motion while the denominator is the effective moment of inertia of the mass-pulley system as a whole.
Conservation of angular momentum
A spinning figure skater starts from an initial angular velocity of $\omega_i=12$[rad/s] with her arms far away from her body. The moment of inertia of her body in this configuration is $I_i=3$[kg$\:$m$^2$]. She then brings her arms close to her body and in the process her moment of inertia changes to $I_f=0.5$[kg$\:$m$^2$]. What will be her new angular velocity?
We will solve this problem using the law of conservation of angular momentum: \[ L_i = L_f \qquad \Rightarrow \qquad I_i\omega_i = I_f \omega_f, \] which we can solve for the final angular velocity $\omega_f$. The answer is $\omega_f = I_i\omega_i/I_f= 3\times 12/0.5=72$[rad/s], which corresponds to 11.46 turns per second.
Conservation of energy
A 14[in] bicycle wheel with mass $m=4$[kg] with all its mass concentrated near the rim is set in rolling motion at a velocity of 20[m/s] up an incline. How far up the incline will the wheel reach before it stops?
We will solve this problem using the principle of conservation of energy $\sum E_i = \sum E_f$. We must take into account both the linear and rotational kinetic energies of the wheel: \[ \begin{align*} K_i \ \ + \ \ K_{ri} \ + U_i & = K_f + K_{rf} + U_f \nl \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2 + 0 \ & = \ 0 \ + \ 0 \ + mgh. \end{align*} \]
The first step is to calculate $I_{wheel}$ using the formula $I_{wheel} = mR^2 = 4 \times (0.355)^2=0.5$[kg m$^2$]. If the linear velocity of the wheel is 20[m/s], then its angular velocity is $\omega=v_t/R=20/0.355=56.34$[rad/s]. We can now use these values in the energy equation: \[ \frac{1}{2}(4)(20)^2 + \frac{1}{2}(0.5)(56.34)^2 + 0 = 800.0 + 793.55 = (4)(9.81)h. \] The maximum height reached will be $h=40.61$[m].
Note that roughly half of the kinetic energy of the wheel was stored in the rotational motion. This shows that it is important to take into account $K_r$ when solving problems using energy principles.
Static equilibrium
We say that a system is in equilibrium when all the forces and torques acting on the system balance each other out. Since there is no net force on the system, it will just sit there motionless.
Conversely, if you see an object that is not moving, then the forces on it must be in equilibrium: \[ \sum F_x = 0, \quad \sum F_y = 0, \quad \sum \mathcal{T} = 0. \] There must be zero net force in the $x$ direction, zero net force in the $y$ direction and zero net torque on the object.
Example: Walking the plank
A heavy wooden plank is placed so that one third of its length protrudes from the side of a pirate ship. The plank has a length of 12[m] and total weight 120[kg]: this means that 40[kg] of its weight is suspended above the ocean, while 80[kg] is lying on the ship's deck. How far out on the plank can a 80[kg] person walk before the plank tips over?
We will use the torque equilibrium equation $\sum \mathcal{T}_E = 0$ where we calculate the torques relative to the edge of the ship. The torque produced by person when he has walked a distance of $x$[m] from the edge of ship is $\mathcal{T}_1 = -80x$. The torque produced by the weight of the plank is given by $\mathcal{T}_2=120\times 2=240$[N$\:$m] since the weight acts in the centre of gravity of the plank, which is located $2$[m] from the edge. The maximum distance that can be walked before the plank tips over is therefore $x=240/80=3$[m]. After that it is all sharks.
Discussion
Our coverage of the ideas of rotational motion has been very brief. The reason for this, is that there was no new physics to be learned. In this section we used the techniques and ideas developed in the context of linear motion to describe the rotational motion of objects.
 It is really important that you see the parallels between
the new rotational concepts and their linear counterparts.
To help you see the connections,
you can compare the diagram shown on the right with the diagram from the beginning of this section.
It is really important that you see the parallels between
the new rotational concepts and their linear counterparts.
To help you see the connections,
you can compare the diagram shown on the right with the diagram from the beginning of this section.
Let us summarize. If you know the torque acting on an object, then you can calculate its angular acceleration $\alpha$. Knowing the angular acceleration $\alpha(t)$ and the initial conditions $\theta_i$ and $\omega_i$, you can then calculate the equations of motion $\omega(t)$ and $\theta(t)$ at all times.
Furthermore, the angular velocity $\omega$ is related to the angular momentum $L=I\omega$ and the rotational kinetic energy $K_r=\frac{1}{2}I \omega^2$ of the rotating object. The angular momentum measures the “quantity of rotational motion”, while the rotational kinetic energy measures how much energy the object has by virtue of its rotational motion.
The moment of inertia $I$ plays the role of the mass $m$ in the rotational equations. In the equation $\mathcal{T}=I\alpha$, the moment of inertia $I$ measures how difficult it is to make the object turn. The moment of inertia also appears in the formulas for the angular momentum and rotational kinetic energy.
Simple harmonic motion
Vibrations and oscillations are all around us. White light is made up of many oscillations of the electromagnetic field at different frequencies (colors). Sounds are made up of a combination of many air vibrations with different frequencies and strengths. In this section we will learn about simple harmonic motion, which describes the oscillation of a mechanical system at a fixed frequency and with a constant amplitude. By studying oscillations in their simplest form, you will pick up important intuition which you can apply to all other types of oscillations.
 The canonical example of simple harmonic motion is the motion of a mass-spring system
illustrated in the figure on the right. The block is free to slide along
the horizontal frictionless surface. If the system is disturbed from its
equilibrium position, it will start to oscillate back and forth at
a certain natural frequency, which depends on the mass of the block and the stiffness of the spring.
The canonical example of simple harmonic motion is the motion of a mass-spring system
illustrated in the figure on the right. The block is free to slide along
the horizontal frictionless surface. If the system is disturbed from its
equilibrium position, it will start to oscillate back and forth at
a certain natural frequency, which depends on the mass of the block and the stiffness of the spring.
In this section we will focus our attention on two mechanical systems: the mass-spring system and the simple pendulum. We will follow the usual approach and describe the positions, velocities, accelerations and energies associated with this type of motion. The notion of simple harmonic motion (SHM) is far more important than just these two systems. The equations and intuition developed for the analysis of the oscillation of these simple mechanical systems can be applied much more generally to sound oscillations, electric current oscillations and even quantum oscillations. Pay attention, that is all I am saying.
Concepts
- $A$: The amplitude of the movement, how far the object goes back and forth relative to the centre position.
- $x(t)$[m], $v(t)$[m/s], $a(t)$[m/s$^2$]: The position, velocity and acceleration of the object as functions of time.
- $T$[s]: The period of the motion, i.e., how long it takes for the motion to repeat.
- $f$[Hz]: The frequency of the motion.
- $\omega$[rad/s]: The angular frequency of the simple harmonic motion.
- $\phi$[rad]: The phase constant. The Greek letter $\phi$ is pronounced “phee”.
Simple harmonic motion
 The figure on the right illustrates a mass-spring system undergoing simple harmonic motion.
Observe that the position of the mass as a function of time behaves like the cosine function.
From the diagram, we can also identify two important parameters of the motion: the amplitude $A$,
which describes the maximum displacement of the mass from the centre position,
and the period $T$, which describes how long it takes for the mass to come back to its initial position.
The figure on the right illustrates a mass-spring system undergoing simple harmonic motion.
Observe that the position of the mass as a function of time behaves like the cosine function.
From the diagram, we can also identify two important parameters of the motion: the amplitude $A$,
which describes the maximum displacement of the mass from the centre position,
and the period $T$, which describes how long it takes for the mass to come back to its initial position.
The equation which describes the position of the object as a function of time is the following: \[ x(t)=A\cos(\omega t + \phi). \] The constant $\omega$ (omega) is called the angular frequency of the motion. It is related to the period $T$ by the equation $\omega = \frac{2\pi}{T}$. The additive constant $\phi$ (phee) is called the phase constant or phase shift and its value depends on the initial condition for the motion $x_i\equiv x(0)$.
I don't want you to be scared by the formula for simple harmonic motion. I know there are a lot of Greek letters that appear in it, but it is actually pretty simple. In order to understand the purpose of the three parameters $A$, $\omega$ and $\phi$, we will do a brief review of the properties of the $\cos$ function.
Review of sin and cos functions
 The functions $f(t)=\sin(t)$ and $f(t)=\cos(t)$ are periodic functions
which oscillate between $-1$ and $1$ with a period of $2\pi$.
Previously we used the functions $\cos$ and $\sin$ in order to find the horizontal and vertical components of vectors,
and called the input variable $\theta$ (theta).
However, in this section the input variable is the time $t$ measured in seconds.
Look carefully at the plot of the function $\cos(t)$.
As $t$ goes from $t=0$ to $t=2\pi$, the function $\cos(t)$ completes one full cycle.
The period of $\cos(t)$ is $T=2\pi$ because this is how long it takes
(in radians) for a point to go around the unit circle.
The functions $f(t)=\sin(t)$ and $f(t)=\cos(t)$ are periodic functions
which oscillate between $-1$ and $1$ with a period of $2\pi$.
Previously we used the functions $\cos$ and $\sin$ in order to find the horizontal and vertical components of vectors,
and called the input variable $\theta$ (theta).
However, in this section the input variable is the time $t$ measured in seconds.
Look carefully at the plot of the function $\cos(t)$.
As $t$ goes from $t=0$ to $t=2\pi$, the function $\cos(t)$ completes one full cycle.
The period of $\cos(t)$ is $T=2\pi$ because this is how long it takes
(in radians) for a point to go around the unit circle.
Time-scaling
To describe periodic motion with a different period, we can still use the $\cos$ function but we must add a multiplier in front of the variable $t$ inside the $\cos$ function. This multiplier is called the angular frequency and is usually denoted $\omega$ (omega). The input-scaled $\cos$ function: \[ f(t) = \cos(\omega t ), \] has a period of $T=\frac{2\pi}{\omega}$.
If you want to have a periodic function with period $T$, you should use the multiplier constant $\omega = \frac{2\pi}{T}$ inside the $\cos$ function. When you vary $t$ from $0$ to $T$, the function $\cos(\omega t )$ will go through one cycle because the quantity $\omega t$ goes from $0$ to $2\pi$. You shouldn't just take my word for this: try this for yourself by building a cos function with a period of 3 units.
The frequency of periodic motion describes how many times per second the motion repeats. The frequency is equal to the inverse of the period: \[ f=\frac{1}{T}=\frac{\omega}{2\pi} \text{ [Hz].} \] The relation between $f$ (frequency) and $\omega$ (angular frequency) is a factor of $2\pi$. This multiplier is needed since the natural cycle length of the $\cos$ function is $2\pi$ radians.
Output-scaling
If we want to have oscillations that go between $-A$ and $+A$ instead of between $-1$ and $+1$, we can multiply the $\cos$ function by the appropriate amplitude: \[ f(t)=A\cos(\omega t). \] The above function has period $T=\frac{2\pi}{\omega}$ and oscillates between $-A$ and $A$ on the $y$ axis.
Time-shifting
The function $A\cos(\omega t)$ starts from its maximum value at $t=0$. In the case of the mass-spring system, this corresponds to the case when the motion begins with the spring maximally stretched $x_i\equiv x(0)=A$.
In order to describe other starting positions for the motion, it may be necessary to introduce a phase shift inside the $\cos$ function: \[ f(t)=A\cos(\omega t + \phi). \] The constant $\phi$ must be chosen so that at $t=0$, the function $f(t)$ correctly describes the initial position of the system.
For example, if the harmonic motion starts from the centre $x_i \equiv x(0)=0$ and is initially going in the positive direction, then the equation of motion is described by the function $A\sin(\omega t)$. However, since $\sin(\theta)=\cos(\theta - \frac{\pi}{2})$ we can equally well describe the motion in terms of a shifted $\cos$ function: \[ x(t) = A\cos\!\left(\omega t - \frac{\pi}{2}\right) = A\sin(\omega t). \] Note that the function $x(t)$ correctly describes the initial position: $x(0)=0$.
By now, the meaning of all the parameters in the simple harmonic motion equation should be clear to you. The constant in front of the $\cos$ tells us the amplitude $A$ of the motion, the multiplicative constant $\omega$ inside the $\cos$ is related to the period/frequency of the motion $\omega = \frac{2\pi}{T} = 2\pi f$. Finally, the additive constant $\phi$ is chosen depending on the initial conditions.
Mass and spring
OK, enough math. It is time to learn about the first physical system which exhibits simple harmonic motion: the mass-spring system.
An object of mass $m$ is attached to a spring with spring constant $k$. If disturbed from rest, this mass-spring system will undergo simple harmonic motion with angular frequency: \[ \omega = \sqrt{ \frac{k}{m} }. \] A stiff spring attached to a small mass will result in very rapid oscillations. A weak spring or a large mass will result in slow oscillations.
A typical exam question will tell you $k$ and $m$ and ask about the period $T$. If you remember the definition of $T$, you can easily calculate the answer: \[ T = \frac{2\pi}{\omega} = 2\pi \sqrt{ \frac{m}{k} }. \]
Equations of motion
The general equations of motion for the mass-spring system are as follows: \[ \begin{align} x(t) &= A\cos(\omega t + \phi), \nl v(t) &= -A\omega \sin(\omega t + \phi), \nl a(t) &= -A\omega^2\cos(\omega t + \phi). \end{align} \]
The general shape of the function $x(t)$ is $\cos$-like. The angular frequency $\omega$ parameter is governed by the physical properties of the system. The parameters $A$ and $\phi$ describe the specifics of the motion, namely, the size of the oscillation and where it starts from.
The function $v(t)$ is obtained, as usual, by taking the derivative of $x(t)$. The function $a(t)$ is obtained by taking the derivative of $v(t)$, which corresponds to the second derivative of $x(t)$.
Motion parameters
The velocity and the acceleration of the object are also periodic functions.
We can find the maximum values of the velocity and the acceleration by reading off the coefficient in front of the $\sin$ and $\cos$ in the functions $v(t)$ and $a(t)$.
- The maximum velocity of the object is
\[ v_{max} = A \omega. \]
- The maximum acceleration is
\[ a_{max} = A \omega^2. \] The velocity is maximum as the object passes through the centre, while the acceleration is maximum when the spring is maximally stretched (compressed).
You will often be asked to solve for the quantities $v_{max}$ and $a_{max}$ in exercises and exams. This is an easy task if you remember the above formulas and you know the values of the amplitude $A$ and the angular frequency $\omega$.
Energy
The potential energy stored in a spring which is stretched (compressed) by a length $x$ is given by the formula $U_s=\frac{1}{2}k x^2$. Since we know $x(t)$, we can obtain the potential energy of the mass-spring system as a function of time: \[ U_s(t)= \frac{1}{2} kx(t)^2 =\frac{1}{2}kA^2\cos^2(\omega t +\phi). \] The potential energy reaches its maximum value $U_{s,max}=\frac{1}{2}kA^2$ when the spring is fully stretched or fully compressed.
The kinetic energy of the mass as a function of time is given by: \[ K(t)= \frac{1}{2} mv(t)^2 = \frac {1}{2}m\omega^2A^2\sin^2(\omega t +\phi). \] The kinetic energy is maximum when the mass passes through the centre position. The maximum kinetic energy is given by $K_{max} = \frac{1}{2} mv_{max}^2= \frac{1}{2}mA^2\omega^2$.
Conservation of energy
The conservation of energy equation tells us that the total energy of the mass-spring system is conserved. The sum of the potential energy and the kinetic energy at any two instants $t_1$ and $t_2$ is the same: \[ U_{s1} + K_2 = U_{s2} + K_2. \]
It is also useful to calculate the total energy of the system $E_T = U_s(t) + K(t) = \text{const}$. This means that even if $U_s(t)$ and $K(t)$ change over time, the total energy of the system always remains constant.
We can use the identity $\cos^2\theta + \sin^2\theta =1$ to verify that the total energy is indeed a constant and that it is equal $U_{s,max}$ and $K_{max}$: \[ \begin{align} E_{T} &= U_s(t) + K(t) \nl &= \frac{1}{2}kA^2\cos^2(\omega t) + \frac {1}{2}m\omega^2A^2\sin^2(\omega t) \nl &= \frac{1}{2}m\omega^2A^2\cos^2(\omega t ) + \frac {1}{2}m\omega^2A^2\sin^2(\omega t ) \ \ \ (\text{since } k = m\omega^2 )\nl &= \frac{1}{2}m\underbrace{\omega^2A^2}_{v_{max}^2}\underbrace{\left[ \cos^2(\omega t) + \sin^2(\omega t)\right]}_{=1} = \frac{1}{2}mv_{max}^2 = K_{max} \nl & =\frac{1}{2}m(\omega A)^2 = \frac{1}{2}(m \omega^2) A^2 =\frac{1}{2}kA^2 = U_{s,max}. \end{align} \]
The best way to understand SHM is to visualize how the energy of the system shifts between the potential energy of the spring and the kinetic energy of the moving mass. When the spring is maximally stretched $x=\pm A$, the mass will have zero velocity and hence zero kinetic energy $K=0$. At this moment all the energy of the system is stored in the spring $E_T= U_{s,max}$. The other important moment is when the mass has zero displacement but maximal velocity $x=0, U_s=0, v=\pm A\omega, E_T=K_{max}$, which corresponds to all the energy being stored as kinetic energy.
Pendulum motion
We now turn our attention to another simple mechanical system whose motion is also described by the simple harmonic motion equations.
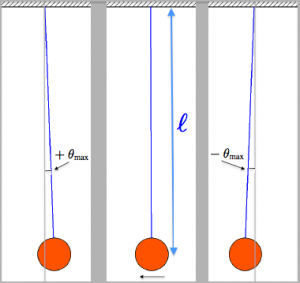 Consider a mass suspended at the end of a long string of length $\ell$ in a gravitational field of strength $g$.
If we start the pendulum from a certain angle $\theta_{max}$ away from the vertical position and then release it,
the pendulum will swing back and forth undergoing simple harmonic motion.
Consider a mass suspended at the end of a long string of length $\ell$ in a gravitational field of strength $g$.
If we start the pendulum from a certain angle $\theta_{max}$ away from the vertical position and then release it,
the pendulum will swing back and forth undergoing simple harmonic motion.
The period of oscillation is given by the following formula: \[ T = 2\pi \sqrt{ \frac{\ell}{g} }. \] Note that the period does not depend on the amplitude of the oscillation (how far the pendulum swings) nor the mass of the pendulum. The only factor that plays a role is the length of the string $\ell$. The angular frequency for a pendulum of length $\ell$ is going to be: \[ \omega \equiv \frac{2\pi}{T} = \sqrt{ \frac{g}{\ell} }. \]
We describe the position of the pendulum in terms of the angle $\theta$ that it makes with the vertical. The equations of motion are described in terms of angular variables: the angular position $\theta$, the angular velocity $\omega_\theta$ and the angular acceleration $\alpha_\theta$: \[ \begin{align} \theta(t) &= \theta_{max} \: \cos\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right), \nl \omega_\theta(t) &= -\theta_{max}\sqrt{ \frac{g}{\ell} } \: \sin\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right), \nl \alpha_\theta(t) &= -\theta_{max}\frac{g}{\ell} \: \cos\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right). \end{align} \] The angle $\theta_{max}$ describes the maximum angle that the pendulum swings to. Note how we had to use a new variable name $\omega_\theta$ for the angular velocity of the pendulum $\omega_\theta(t)=\frac{d}{dt}\!\left(\theta(t)\right)$, so as not to confuse it with the constant $\omega=\sqrt{ \frac{g}{\ell} }$ inside the $\cos$ function, which describes angular frequency of the periodic motion.
Energy
The motion of the pendulum is best understood by imagining how the energy of the system shifts between the gravitational potential energy of the mass and its kinetic energy.
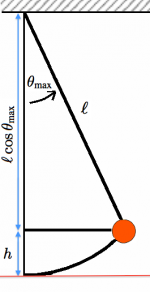 The pendulum will have a maximum potential energy when it swings to the side by the angle $\theta_{max}$.
At that angle, the vertical position of the mass will be increased by a height $h$ above the lowest point.
We can calculate $h$ as follows:
\[
h = \ell - \ell \cos \theta_{max}.
\]
Thus the maximum gravitational potential energy of the mass is therefore:
\[
U_{g,max}= mgh= mg\ell(1-\cos\theta_{max}).
\]
The pendulum will have a maximum potential energy when it swings to the side by the angle $\theta_{max}$.
At that angle, the vertical position of the mass will be increased by a height $h$ above the lowest point.
We can calculate $h$ as follows:
\[
h = \ell - \ell \cos \theta_{max}.
\]
Thus the maximum gravitational potential energy of the mass is therefore:
\[
U_{g,max}= mgh= mg\ell(1-\cos\theta_{max}).
\]
By the conservation of energy principle, the maximum kinetic energy of the pendulum must be equal to the maximum of the gravitational potential energy: \[ mg\ell(1-\cos\theta_{max}) = U_{g,max} = K_{max} = \frac{1}{2} mv_{max}^2, \] where $v_{max}=\ell \omega_\theta$ is the linear velocity of the mass as it swings through the centre.
Explanations
It is worthwhile to understand how the equations of simple harmonic motion come about. In this subsection, we will discuss how the equations are derived from Newton's second law $F=ma$.
Trigonometric derivatives
The slope (derivative) of the function $\sin(t)$ varies between $-1$ and $1$. The slope is largest when $\sin$ passes through the $x$ axis and the slope is zero when it reaches its maximum and minimum values. A careful examination of the graphs of the bare functions $\sin$ and $\cos$ reveals that the derivative of the function $\sin(t)$ is described by the function $\cos(t)$ and vice versa: \[ f(t) = \sin(t) \:\qquad \Rightarrow \qquad f'(t) = \cos(t), \] \[ f(t) = \cos(t) \qquad \Rightarrow \qquad f'(t) = -\sin(t). \] When you learn more about calculus you will know how to find the derivative of any function you want, but for now just take my word that the above two formulas are true.
The chain rule for derivatives tells us that the derivative of a composite function $f(g(x))$ is given by $f'(g(x))\cdot g'(x)$, i.e., you must take the derivative of the outer function and then multiply by the derivative of the inner function. We can use the chain rule to the find derivative of the simple harmonic motion position function: \[ x(t)=A\cos(\omega t +\phi) \ \ \Rightarrow \ \ v(t) \equiv x^{\prime}(t)=-A\sin(\omega t +\phi)(\omega) = -A\omega\sin(\omega t +\phi), \] where the outer function is $f(x)=A\cos(x)$ with derivative $f'(x)=-A\sin(x)$ and the inner function is $g(x)=\omega x +\phi$ with derivative $g'(x)=\omega$.
The same reasoning is used to obtain the second derivative: \[ a(t)\equiv \frac{d}{dt}\!\left\{ v(t) \right\} =-A\omega^2 \cos(\omega t +\phi) = -\omega^2 x(t). \] Note that $a(t)=x^{\prime\prime}(t)$ has the same form as $x(t)$, but always acts in the opposite direction.
I hope this clarifies for you how we obtained the functions $v(t)$ and $a(t)$: we simply took the derivative of the function $x(t)$.
Derivation of the mass-spring SHM equation
You may be wondering where the equation $x(t)=A\cos(\omega t + \phi)$ comes from. This formula looks very different from the kinematics equations for linear motion $x(t) = x_i + v_it + \frac{1}{2}at^2$, which we obtained starting from Newton's second law $F=ma$ after two integration steps.
In this section, we pulled the $x(t)=A\cos(\omega t + \phi)$ formula out of thin air, as if by revelation. Why did we suddenly start talking about $\cos$ functions and Greek letters with dubious names like phase. Are you phased by all of this? When I was first learning about simple harmonic motion, I was totally phased because I didn't see where the $\sin$ and $\cos$ came from.
The $\cos$ also comes from $F=ma$, but the story is a little more complicated this time. The force exerted by a spring is $F_{s} = -kx$. If you draw a force diagram on the mass, you will see that the force of the spring is the only force acting on it so we have: \[ \sum F = F_s =ma \qquad \Rightarrow \qquad -kx = ma. \] Recall that the acceleration is the second derivative of the position: \[ a=\frac{dv(t)}{dt} = \frac{d^2x(t)}{dt^2} = x^{\prime\prime}(t). \]
We now rewrite the equation $-kx = ma$ in terms of the function $x(t)$ and its second derivative: \[ \begin{align*} -kx(t) &= m\frac{d^2x(t)}{dt^2} \nl 0 & = m\frac{d^2x(t)}{dt^2}+ kx(t) \nl 0 & = \frac{d^2x(t)}{dt^2}+ \frac{k}{m}x(t). \end{align*} \]
This is called a differential equation. Instead of looking for an unknown number as in normal equations, in differential equations we are looking for an unknown function $x(t)$. We do not know what $x(t)$ is but we do know one of its properties, namely, that its second derivative $x^{\prime\prime}(t)$ is equal to the negative of $x(t)$ multiplied by some constant.
To solve a differential equation, you have to guess which function $x(t)$ satisfies this property. There is an entire course called Differential Equations, in which engineers and physicists learn how to do this guessing thing. Can you think of a function which, when multiplied by $\frac{k}{m}$, is equal to its second derivative?
OK, I thought of one: \[ x_1(t)=A_1 \cos\!\left( \sqrt{ \frac{k}{m}}t \right). \] Come to think of it, there is also a second one which works: \[ x_2(t)=A_2 \sin\!\left( \sqrt{ \frac{k}{m}}t \right). \] You should try this for yourself: verify that $x^{\prime\prime}_1(t) + \frac{k}{m}x_1(t)=0$ and $x^{\prime\prime}_2(t) + \frac{k}{m}x_2(t)=0$, which means that these functions are both solutions to the differential equation $x^{\prime\prime}(t)+\frac{k}{m} x(t)=0$. Since both $x_1(t)$ and $x_2(t)$ are solutions, any combination of them must also be a solution: \[ x(t) = A_1\cos(\omega t) + A_2\sin(\omega t). \] This is kind of the answer we were looking for. I say kind of because the function $x(t)$ is specified in terms of the coefficients $A_1$ and $A_2$ instead of the usual parameters: the amplitude $A$ and a phase $\phi$.
Lo and behold, using the trigonometric identity $\cos(a + b)=\cos(a)\cos(b) - \sin(a)\sin(b)$ we can express the function $x(t)$ as a time-shifted trigonometric function: \[ x(t)=A\cos(\omega t + \phi) = A_1\cos(\omega t) + A_2\sin(\omega t). \] The expression on the left is the preferred way of describing SHM because the parameters $A$ and $\phi$ corresponds to observable aspects of the motion.
Let me go over what just happened here one more time. Our goal was to find the equation of motion which predicts the position of an object as a function of time $x(t)$. To understand what is going on, let us draw an analogy with a situation which we have seen previously. In linear kinematics, uniform accelerated motion with $a(t)=a$ is described by the equation $x(t)=x_i+v_it + \frac{1}{2}at^2$ in terms of parameters $x_i$ and $v_i$. Depending on the initial velocity and the initial position of the object, we obtain different trajectories. Simple harmonic motion with angular frequency $\omega$ is described by the equation $x(t)=A\cos(\omega t + \phi)$ in terms of the parameters $A$ and $\phi$, which are the natural parameters for describing SHM. We obtain different harmonic motion trajectories depending on the values of the parameters $A$ and $\phi$.
Derivation of the pendulum SHM equation
To see how the SHM equation of motion arises in the case of the pendulum, we need to start from the torque equation $\mathcal{T}=I\alpha$.
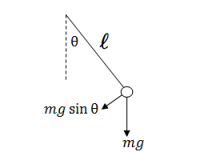 The diagram on the right illustrates how we can calculate the torque on the pendulum
which is caused by the force of gravity as a function of the displacement angle $\theta$.
Recall that the torque calculation only takes into account the $F_{\!\perp}$ component
of any force, since it is the only part which causes rotation:
\[
\mathcal{T}_\theta = F_{\!\perp} \ell = mg\sin\theta \ell.
\]
If we now substitute this into the equation $\mathcal{T}=I\alpha$,
we obtain the following:
\[
\begin{align*}
\mathcal{T} &= I \alpha \nl
mg\sin\theta(t) \ell &= m\ell^2 \frac{d^2\theta(t)}{dt^2} \nl
g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2}
\end{align*}
\]
The diagram on the right illustrates how we can calculate the torque on the pendulum
which is caused by the force of gravity as a function of the displacement angle $\theta$.
Recall that the torque calculation only takes into account the $F_{\!\perp}$ component
of any force, since it is the only part which causes rotation:
\[
\mathcal{T}_\theta = F_{\!\perp} \ell = mg\sin\theta \ell.
\]
If we now substitute this into the equation $\mathcal{T}=I\alpha$,
we obtain the following:
\[
\begin{align*}
\mathcal{T} &= I \alpha \nl
mg\sin\theta(t) \ell &= m\ell^2 \frac{d^2\theta(t)}{dt^2} \nl
g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2}
\end{align*}
\]
What follows is something which is not mathematically rigorous, but will allow us to continue and solve this problem. When $\theta$ is a small angle we can use the following approximation: \[ \sin(\theta)\ \approx \ \theta, \qquad \qquad \text{ for } \theta \ll 1. \] This type of equation is called a small angle approximation. You will see where it comes from later on when you learn about Taylor series approximations to functions. For now, you can convince yourself of the above formula by zooming many times on the graph of the function $\sin$ near the origin to see that $y=\sin(x)$ will look very much like $y=x$. Try this out.
Using the small angle approximation for $\sin\theta$ we can rewrite the equation involving $\theta(t)$ and its second derivative as follows: \[ \begin{align*} g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2} \nl g\theta(t) &\approx \ell \frac{d^2\theta(t)}{dt^2} \nl 0 &= \frac{d^2\theta(t)}{dt^2}+ \frac{g}{\ell}\theta(t). \end{align*} \]
At this point we recognize that we are dealing with the same differential equation as in the case of the mass-spring system: $\theta^{\prime\prime}(t)+\omega^2 \theta(t)=0$, which has solution: \[ \theta(t) = \theta_{max}\cos(\omega t + \phi), \] where the constant inside the $\cos$ function is $\omega=\sqrt{\frac{g}{\ell}}$.
Examples
When asked to solve word problems, you will usually be told the initial amplitude $x_i=A$ or the initial velocity $v_i=\omega A$ of the SHM and the question will ask you to calculate some other quantity. Answering these problems shouldn't be too difficult provided you write down the general equations for $x(t)$, $v(t)$ and $a(t)$, fill-in the knowns quantities and then solve for the unknowns.
Standard example
You are observing a mass-spring system build from a $1$[kg] mass and a 250[N/m] spring. The amplitude of the oscillation is 10[cm]. Determine (a) the maximum speed of the mass, (b) the maximum acceleration, and (c ) the total mechanical energy of the system.
First we must find the angular frequency for this system $\omega = \sqrt{k/m}=\sqrt{250/1}=15.81$[rad/s]. To find (a) we use the equation $v_{max} = \omega A = 15.81 \times 0.1=1.58$[m/s]. Similarly, we can find the maximum acceleration using $a_{max} = \omega^2 A = 15.81^2 \times 0.1=25$[m$^2$/s]. There are two equivalent ways for solving (c ). We can obtain the total energy of the system by considering the potential energy of the spring when it is maximally extended (compressed) $E_T=U_s(A) = \frac{1}{2}kA^2 = 1.25$[J], or we can obtain the total energy from the maximum kinetic energy $E_T=K=\frac{1}{2}m v_{max}^2 = 1.25$[J].
Discussion
In this section we learned about simple harmonic motion, which is described by the equation $x(t)=A\cos(\omega t + \phi)$. You may be wondering what non-simple harmonic motion is. A simple extension of what we learned would be to study oscillating systems where the energy is slowly dissipating. This is known as damped harmonic motion for which the equation of motion looks like $x(t)=Ae^{-\gamma t}\cos(\omega t + \phi)$, which describes an oscillation whose magnitude slowly decreases. The coefficient $\gamma$ is known as the damping coefficient and indicates how fast the energy of the system is dissipated.
The concept of SHM comes up in many other areas of physics. When you learn about electric circuits, capacitors and inductors, you will run into equations of the form $v^{\prime\prime}(t)+\omega^2 v(t)=0$, which indicates that the voltage in a circuit is undergoing simple harmonic motion. Guess what, the same equation used to describe the mechanical motion of the mass-spring system will be used to describe the voltage in an oscillating circuit!
Links
[ Plot of the simple harmonic motion using a can of spray-paint. ]
http://www.youtube.com/watch?v=p9uhmjbZn-c
NOINDENT
[ 15 pendulums with different lengths. ]
http://www.youtube.com/watch?v=yVkdfJ9PkRQ